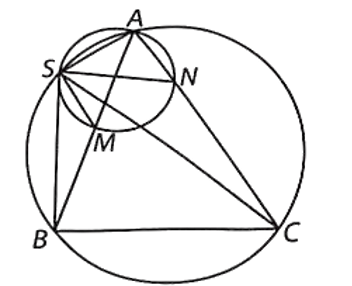
Cho tam giác ABC nội tiếp đường tròn (O). Trên các cạnh AB, AC lần lượt lấy các điểm
Cho tam giác ABC nội tiếp đường tròn (O). Trên các cạnh AB, AC lần lượt lấy các điểm M và N (M khác A và B, N khác A và C). Giả sử đường tròn ngoại tiếp tam giác AMN cắt đường tròn (O) tại một điểm S khác A. Chứng minh rằng
Giải vở thực hành Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác - Kết nối tri thức
Bài 8 trang 94 VTH Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O). Trên các cạnh AB, AC lần lượt lấy các điểm M và N (M khác A và B, N khác A và C). Giả sử đường tròn ngoại tiếp tam giác AMN cắt đường tròn (O) tại một điểm S khác A. Chứng minh rằng
Lời giải:
Vì và là các góc nội tiếp của đường tròn nội tiếp tam giác AMN và cùng chắn cung nên Từ đây suy ra
(1)
Xét tam giác SBM và tam giác SCN, ta có:
(hai góc nội tiếp của (O) cùng chắn cung ),
(theo chứng minh trên).
Vậy ∆SBM ᔕ ∆SCN (g.g). Suy ra hay
Lời giải vở thực hành Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác hay khác: