Bài 6 trang 32 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 1: Phương pháp quy nạp toán học

Haylamdo biên soạn và sưu tầm lời giải Bài 6 trang 32 Chuyên đề Toán 10 trong Bài 1: Phương pháp quy nạp toán học. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Bài 6 trang 32 Chuyên đề Toán 10: Trong mặt phẳng, cho đa giác A₁ A₂ A₃... A_n có n cạnh (n ≥ 3). Gọi S_n là tổng số đo các góc trong của đa giác.

a) Tính S₃, S₄, S₅ tương ứng với trường hợp đa giác là tam giác, tứ giác, ngũ giác.

b) Từ đó, dự đoán công thức tính S_n và chứng minh công thức đó bằng phương pháp

Lời giải:

a) S₃ = 180^o, S₄ = 360^o, S₅ = 540^o.

b) Từ a) ta dự đoán S_n = (n – 2) . 180^o.

Ta chứng minh công thức bằng phương pháp quy nạp toán học.

Bước 1. Với n = 3, ta có tổng ba góc của một tam giác bằng 180^o = (3 – 2) . 180^o. Vậy công thức đúng với n=3.

Bước 2. Giả sử công thức đúng với n = k ≥ 3, ta sẽ chứng minh công thức đúng với n = k + 1.

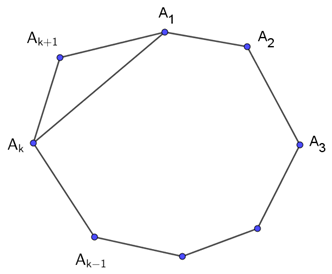
Thật vậy, xét đa giác k + 1 cạnh A₁A₂...A_kA_{k + 1}, nối hai đỉnh A₁ và A_k ta được đa giác k cạnh A₁A₂...A_k. Theo giả thiết quy nạp, tồng các góc của đa giác k cạnh này bằng (k – 2) . 180^o

Dễ thấy tổng các góc của đa giác A₁A₂...A_kA_{k + 1} bằng tổng các góc của đa giác

A₁A₂...A_k cộng với tổng các góc của tam giác A_{k + 1}A_kA₁, tức là bằng

(k – 2) . 180^o + 180^o = (k – 1) . 180^o = [(k+1) – 2] . 180^o.

Vậy công thức đúng với mọi đa giác n cạnh, n ≥ 3.