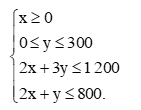Bài 2.2 trang 32 Chuyên đề Toán 12
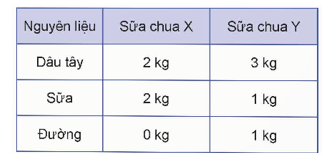
Một cơ sở sản xuất hai loại sữa chua X và Y. Nguyên liệu chính để sản xuất hai loại sữa chua này là dâu tây, sữa và đường. Để sản xuất một đơn vị sữa chua X và một đơn vị sữa chua Y cần lượng nguyên liệu như trong bảng:
Giải Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính - Kết nối tri thức
Bài 2.2 trang 32 Chuyên đề Toán 12: Một cơ sở sản xuất hai loại sữa chua X và Y. Nguyên liệu chính để sản xuất hai loại sữa chua này là dâu tây, sữa và đường. Để sản xuất một đơn vị sữa chua X và một đơn vị sữa chua Y cần lượng nguyên liệu như trong bảng:
Nguồn nguyên liệu dự trữ dâu tây, sữa và đường lần lượt là 1,2 tấn; 0,8 tấn và 0,3 tấn. Giá bán mỗi đơn vị sữa chua X và Y lần lượt là 800 nghìn đồng và 1,2 triệu đồng. Cơ sở sản xuất cần sản xuất bao nhiêu đơn vị sữa chua X và Y để lợi nhuận thu được là lớn nhất?
Lời giải:
Đổi 800 nghìn đồng = 0,8 triệu đồng;
1,2 tấn = 1 200 kg; 0,8 tấn = 800 kg; 0,3 tấn = 300 kg.
Gọi x và y lần lượt là số đơn vị sữa chua X và Y cần sản xuất.
Lợi nhuận thu được là: 0,8x + 1,2y (triệu đồng).
Hệ bất phương trình ràng buộc x và y là
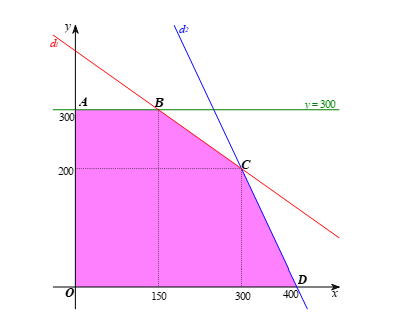
Miền nghiệm của hệ bất phương trình này là miền ngũ giác OABCD được tô màu như hình vẽ dưới đây:
Ở đây, d1: 2x + 3y = 1 200 và d2: 2x + y = 800.
Các điểm cực biên là: O(0; 0), A(0; 300), B(150; 300), C(300; 200), D(400; 0).
Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên.
Ta có đường thẳng d1 (hay BC) có phương trình là 2x + 3y = 1 200, nên với mọi điểm M(x; y) thuộc đường thẳng BC ta đều có:
F(x; y) = 0,8x + 1,2y = 0,4(2x+ 3y) = 0,4 . 1 200 = 480.
Vậy biểu thức F(x; y) đạt giá trị lớn nhất bằng 480 tại mọi điểm M(x; y) thuộc đoạn thẳng BC. Như vậy bài toán có vô số phương án tối ưu, đó là tọa độ của tất cả các điểm thuộc đoạn thẳng BC.
Vậy cơ sở sản xuất cần sản xuất x đơn vị sữa chua X và đơn vị sữa chua Y với 150 ≤ x ≤ 300 thì lợi nhuận thu được là lớn nhất.
Lời giải bài tập Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác: