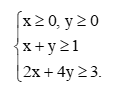Luyện tập 3 trang 32 Chuyên đề Toán 12
Giải bài toán quy hoạch tuyến tính sau:
Giải Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính - Kết nối tri thức
Luyện tập 3 trang 32 Chuyên đề Toán 12: Giải bài toán quy hoạch tuyến tính sau:
F(x; y) = x + 2y → min
với các ràng buộc
Lời giải:
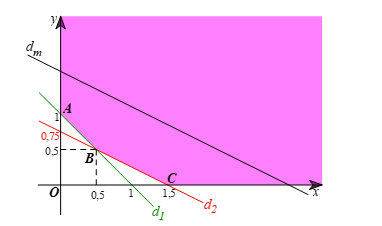
Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
Ở đây, d1, d2 là các đường thẳng có phương trình lần lượt là x + y = 1 và 2x + 4y = 3.
Có ba điểm cực biên là A(0; 1), B(0,5; 0,5), C(1,5; 0).
Với mỗi số thực m, xét đường thẳng dm: x + 2y = m.
Đường thẳng dm song song với đường thẳng d2 (hay BC) và cắt Oy tại điểm Dễ thấy dm ∩ S ≠ 0 nếu và chỉ nếu hay m ≥ 1,5.
Từ đó suy ra, giá trị nhỏ nhất của G(x; y) bằng 1,5, đạt được tại mọi điểm của đoạn BC.
Thực tế, mọi điểm M (x; y) thuộc đoạn BC ta đều có:
Cũng từ kết quả dm ∩ S ≠ 0 nếu và chỉ nếu m ≥ 1,5 suy ra F(x; y) không có giá trị lớn nhất trên miền S. Thực tế, F(x; y) có thể lớn tùy ý khi x, y đủ lớn.
Lời giải bài tập Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác: