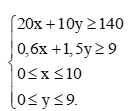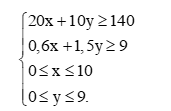Luyện tập 1 trang 26 Chuyên đề Toán 12
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất X và 9 kg chất Y. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20 kg chất X và 0,6 kg chất Y. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất X và 1,5 kg chất Y. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Giải Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính - Kết nối tri thức
Luyện tập 1 trang 26 Chuyên đề Toán 12: Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất X và 9 kg chất Y. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20 kg chất X và 0,6 kg chất Y. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất X và 1,5 kg chất Y. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đáp ứng được các yêu cầu đặt ra ở trên?
a) Đặt ẩn và viết bài toán quy hoạch tuyến tính diễn tả yêu cầu của bài toán trên.
b) Biểu diễn tập các phương án chấp nhận được và tìm các phương án cực biên.
Lời giải:
a) Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng (x ≥ 0, y ≥ 0).
Do cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên x ≤ 10, y ≤ 9.
Số kg chất X chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 20x + 10y (kg).
Số kg chất Y chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 0,6x + 1,5y (kg).
Theo bài, cần chiết xuất ít nhất 140 kg chất X và 9 kg chất Y nên ta có hệ phương trình:
Gọi F(x; y) là chi phí mua nguyen liệu, khi đó F(x; y) = 4x + 3y (triệu đồng).
Vậy ta có bài toán quy hoạch tuyến tính như sau:
F(x; y) = 4x + 3y → min
với các ràng buộc
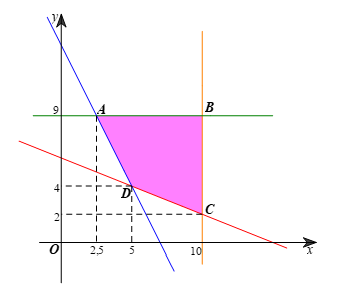
b) Tập các phương án chấp nhận được là miền tô màu trong hình vẽ dưới đây:
Các đỉnh của miền nghiệm là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).
Các phương án cực biên là: (2,5; 9), (10; 9), (10; 2), (5; 4).
Lời giải bài tập Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác: