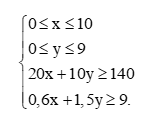Luyện tập 2 trang 29 Chuyên đề Toán 12
Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Phải thuê bao nhiêu xe loại A và bao nhiêu xe loại B để chi phí bỏ ra là ít nhất mà vẫn chở được hết hàng và người?
Giải Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính - Kết nối tri thức
Luyện tập 2 trang 29 Chuyên đề Toán 12: Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Phải thuê bao nhiêu xe loại A và bao nhiêu xe loại B để chi phí bỏ ra là ít nhất mà vẫn chở được hết hàng và người?
Lời giải:
Gọi x và y lần lượt là số xe loại A và loại B cần thuê.
Chi phí thuê xe là: F(x; y) = 4x + 3y (triệu đồng).
Hệ bất phương trình ràng buộc x và y là:
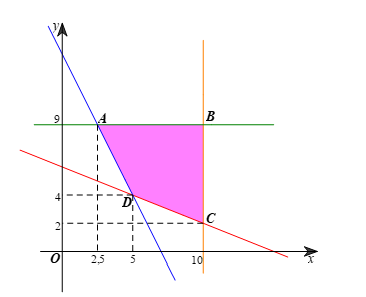
Miền nghiệm của hệ bất phương trình trên là miền tứ giác ABCD trong hình vẽ dưới đây:
Các điểm cực biên là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền tứ giác ABCD. Ta biết rằng F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị củ F(x; y) tại các đỉnh của tứ giác ta được:
F(2,5; 9) = 4.2,5 + 3.9 = 37;
F(10; 9) = 4.10 + 3.9 = 67;
F(10; 2) = 4.10 + 3.2 = 46;
F(5; 4) = 4.5 + 3.4 = 32.
Giá trị nhỏ nhất của F(x; y) bằng 32 tại D(5; 4). Phương án tối ưu là (5; 4).
Vậy phải thuê 5 xe loại A và 4 xe loại B để chi phí bỏ ra là ít nhất (32 triệu đồng) mà vẫn chở được hết hàng và người.
Lời giải bài tập Chuyên đề Toán 12 Bài 3: Vận dụng hệ bất phương trình bậc nhất hai ẩn để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác: