Bài 2 trang 20 Chuyên đề Toán 12 Chân trời sáng tạo

Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1 800 m và chiều sâu 2 m (Hình 7). Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Cần chọn chiều dài và chiều rộng của bể bằng bao nhiêu để tiết kiệm chi phí xây dựng bể nhất?

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu - Chân trời sáng tạo

Bài 2 trang 20 Chuyên đề Toán 12: Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1 800 m³ và chiều sâu 2 m (Hình 7). Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Cần chọn chiều dài và chiều rộng của bể bằng bao nhiêu để tiết kiệm chi phí xây dựng bể nhất?

Lời giải:

Gọi x, y (x > 0, y > 0, tính bằng mét) lần lượt là chiều dài và chiều rộng của bể.

Thể tích của bể là V = 2xy = 1 800 (m³), suy ra $y=\frac{900}{x}$(m).

Diện tích đáy bể là S_đ = xy (m²).

Diện tích thành bể là S_t = 2(x + y) ∙ 2 = 4(x + y) (m²).

Giả sử chi phí để xây mỗi đơn vị diện tích thành bể là a (đồng, a > 0).

Khi đó chi phí để xây mỗi đơn vị diện tích đáy bể là 2a (đồng).

Tổng chi phí để xây bể bơi là

C = 2axy + a ∙ 4(x + y) = $2ax\cdot \frac{900}{x}+4a\left(x+\frac{900}{x}\right)=1800a+4ax+\frac{3600a}{x}$(đồng).

Xét hàm số f(x) = 1800a + 4ax + $\frac{3600a}{x}$ với x ∈ (0; + ∞) và a > 0.

Ta có f'(x) = 4a – $\frac{3600a}{x^2}$;

          f'(x) = 0 ⇔ $4a-\frac{3600a}{x^2}=0\iff x^2=900\iff x=30\in \left(0;+\infty \right)$.

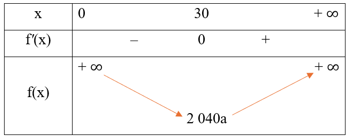
Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }f\left(x\right)=2040a$, đạt được tại x = 30.

Với x = 30 m thì ta có $y=\frac{900}{x}=\frac{900}{30}=30$.

Vậy với chiều rộng và chiều dài của bể bằng nhau và bằng 30 m thì tiết kiệm được chi phí xây dựng bể nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu hay, chi tiết khác:

• Khởi động trang 15 Chuyên đề Toán 12: Một người đang ở vị trí A muốn đi đến vị trí B trên bờ hồ như hình bên ....

• Khám phá trang 15 Chuyên đề Toán 12: Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp ....

• Thực hành 1 trang 17 Chuyên đề Toán 12: Hai nhà máy được đặt tại các vị trí A và B cách nhau 4 km ....

• Thực hành 2 trang 18 Chuyên đề Toán 12: Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài ....

• Thực hành 3 trang 19 Chuyên đề Toán 12: Tại một xưởng sản xuất, chi phí để sản xuất x sản phẩm mỗi tháng là ....

• Thực hành 4 trang 20 Chuyên đề Toán 12: Cơ sở A chuyên cung cấp một loại sản phẩm nông nghiệp X cho nhà phân phối B ....

• Vận dụng trang 20 Chuyên đề Toán 12: Hiện tại, mỗi tháng một cửa hàng đồ lưu niệm bán được 100 sản phẩm A ....

• Bài 1 trang 20 Chuyên đề Toán 12: Người ta muốn xây một đường cống thoát nước có mặt cắt ngang ....

• Bài 3 trang 20 Chuyên đề Toán 12: Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước ....

• Bài 4 trang 21 Chuyên đề Toán 12: Một giếng dầu ngoài khơi được đặt ở vị trí A cách bờ biển 3 km ....

• Bài 5 trang 21 Chuyên đề Toán 12: Tại một xí nghiệp, nếu trong một tuần xí nghiệp sản xuất x nghìn sản phẩm ....