Thực hành 2 trang 18 Chuyên đề Toán 12 Chân trời sáng tạo

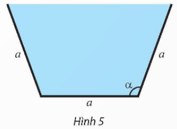
Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài đáy bé bằng độ dài cạnh bên và bằng a (cm) không đổi (Hình 5). Gọi α là một góc của hình thang cân tạo bởi đáy bé và cạnh bên . Tìm α để diện tích mặt cắt ngang của máng lớn nhất.

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu - Chân trời sáng tạo

Thực hành 2 trang 18 Chuyên đề Toán 12: Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài đáy bé bằng độ dài cạnh bên và bằng a (cm) không đổi (Hình 5). Gọi α là một góc của hình thang cân tạo bởi đáy bé và cạnh bên $\left(\frac{\pi }{2}\le \alpha <\pi \right)$. Tìm α để diện tích mặt cắt ngang của máng lớn nhất.

Lời giải:

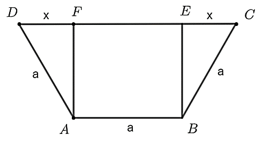
Gọi tên các điểm như hình vẽ dưới đây.

Kẻ các đường cao AF, BE của hình thang cân ABCD.

Ta chứng minh được ABEF là hình chữ nhật và DF = EC.

Khi đó ta có EF = AB = a (cm).

Đặt DF = EC = x (cm, 0 ≤ x < a).

Ta có DC = DF + FE + EC = x + a + x = 2x + a (cm).

Áp dụng định lí Pythagore ta tính được $AF=\sqrt{A{D}^2-D{F}^2}=\sqrt{a^2-x^2}$(cm).

 Diện tích mặt cắt ngang của máng nước hay chính là diện tích hình thang cân ABCD là S = (AB + CD) ∙ AF : 2 = (a + 2x + a) ∙ $\sqrt{a^2-x^2}$: 2 = (a + x)$\sqrt{a^2-x^2}$ (cm²).

Xét hàm số S(x) = (a + x)$\sqrt{a^2-x^2}$ với x ∈ [0; a).

Ta có $S^{\text{'}}\left(x\right)=\sqrt{a^2-x^2}-\left(a+x\right)\frac{x}{\sqrt{a^2-x^2}}=\frac{-2x^2-ax+a^2}{\sqrt{a^2-x^2}}$.

          S'(x) = 0 ⇔ – 2x² – ax + a² = 0 ⇔ (2x – a)(x + a) = 0 ⇔ x = $\frac{a}{2}$ ∈ [0; a).

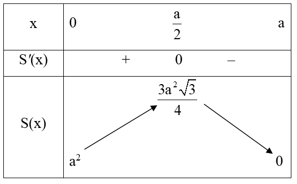
Bảng biến thiên:

Từ bảng biến thiên, ta có $\underset{\left[0;a\right)}{\max }S\left(x\right)=\frac{3a^2\sqrt{3}}{4}$, đạt được tại x = $\frac{a}{2}$.

Khi đó ta có, $\sin \widehat{DAF}=\frac{DF}{DA}=\frac{\frac{a}{2}}{a}=\frac{1}{2}\Rightarrow \widehat{DAF}=\frac{\pi }{6}$.

Suy ra $\widehat{DAB}=\widehat{DAF}+\widehat{FAB}=\frac{\pi }{6}+\frac{\pi }{2}=\frac{2\pi }{3}\in \left[\frac{\pi }{2};\pi \right)$.

Vậy $\alpha =\frac{2\pi }{3}$ thì diện tích mặt cắt ngang của máng lớn nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu hay, chi tiết khác:

• Khởi động trang 15 Chuyên đề Toán 12: Một người đang ở vị trí A muốn đi đến vị trí B trên bờ hồ như hình bên ....

• Khám phá trang 15 Chuyên đề Toán 12: Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp ....

• Thực hành 1 trang 17 Chuyên đề Toán 12: Hai nhà máy được đặt tại các vị trí A và B cách nhau 4 km ....

• Thực hành 3 trang 19 Chuyên đề Toán 12: Tại một xưởng sản xuất, chi phí để sản xuất x sản phẩm mỗi tháng là ....

• Thực hành 4 trang 20 Chuyên đề Toán 12: Cơ sở A chuyên cung cấp một loại sản phẩm nông nghiệp X cho nhà phân phối B ....

• Vận dụng trang 20 Chuyên đề Toán 12: Hiện tại, mỗi tháng một cửa hàng đồ lưu niệm bán được 100 sản phẩm A ....

• Bài 1 trang 20 Chuyên đề Toán 12: Người ta muốn xây một đường cống thoát nước có mặt cắt ngang ....

• Bài 2 trang 20 Chuyên đề Toán 12: Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1 800 m3 và chiều sâu 2 m ....

• Bài 3 trang 20 Chuyên đề Toán 12: Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước ....

• Bài 4 trang 21 Chuyên đề Toán 12: Một giếng dầu ngoài khơi được đặt ở vị trí A cách bờ biển 3 km ....

• Bài 5 trang 21 Chuyên đề Toán 12: Tại một xí nghiệp, nếu trong một tuần xí nghiệp sản xuất x nghìn sản phẩm ....