Khởi động trang 15 Chuyên đề Toán 12 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

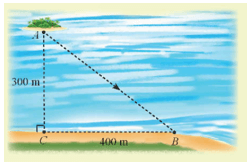
Một người đang ở vị trí A muốn đi đến vị trí B trên bờ hồ như hình bên. Biết rằng người đó chèo thuyền với tốc độ 50 m/phút và chạy bộ với tốc độ 100 m/phút. Nếu người đó chèo thuyền thẳng từ A đến B thì tốn bao nhiêu thời gian? Có phương án nào tốn ít thời gian hơn không?

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu - Chân trời sáng tạo

Khởi động trang 15 Chuyên đề Toán 12: Một người đang ở vị trí A muốn đi đến vị trí B trên bờ hồ như hình bên. Biết rằng người đó chèo thuyền với tốc độ 50 m/phút và chạy bộ với tốc độ 100 m/phút. Nếu người đó chèo thuyền thẳng từ A đến B thì tốn bao nhiêu thời gian? Có phương án nào tốn ít thời gian hơn không?

Khởi động trang 15 Chuyên đề Toán 12

Lời giải:

Sau bài học này, ta giải quyết được bài toán trên như sau:

Áp dụng định lý Pythagore, ta tính được AB = 500 m.

Do đó, nếu người đó chèo thuyền thẳng từ A đến B thì tốn $\frac{500}{50} = 10$ phút.

Ta xem xét phương án sau:

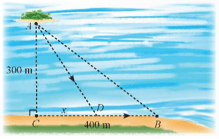
Giả sử người đó chèo thuyền thẳng đến điểm D nằm giữa B và C và cách C một đoạn x (m), rồi chạy bộ thẳng đến B.

Khởi động trang 15 Chuyên đề Toán 12

Ta cần tìm giá trị của x để người đó tốn ít thời gian nhất.

Ta có: $A D = \sqrt{x^{2} + 300^{2}} = \sqrt{x^{2} + 90 000}$ (m); DB = 400 – x (m) với 0 ≤ x ≤ 400.

Thời gian người đó tiêu tốn là

$t = \frac{\sqrt{x^{2} + 90 000}}{50} + \frac{400 - x}{100} = \frac{1}{100} (2 \sqrt{x^{2} + 90 000} + 400 - x)$ (phút).

Xét hàm số $y = 2 \sqrt{x^{2} + 90 000} + 400 - x$ với 0 ≤ x ≤ 400, ta có:

$y^{'} = \frac{2 x}{\sqrt{x^{2} + 90 000}} - 1$ ;

y' = 0 ⇔ $\frac{2 x}{\sqrt{x^{2} + 90 000}} - 1 = 0 \Leftrightarrow 2 x = \sqrt{x^{2} + 90 000}$ ⇔ 4x² = x² + 90 000

⇔ x² = 30 000 ⇔ x = $100 \sqrt{3}$ ∈ [0; 400].

Ta có y(0) = 1 000; $y (100 \sqrt{3}) = 300 \sqrt{3} + 400 \approx 920$ ; y(400) = 1 000.

Vậy $\min_{[0; 400]} y = y (100 \sqrt{3}) \approx 920$ .

Suy ra giá trị nhỏ nhất của t là $\frac{920}{100} = 9,2$ (phút), đạt được khi x = $100 \sqrt{3}$ ≈ 173 (m).

Do đó, người đó tốn ít thời gian nhất khi x = $100 \sqrt{3}$ ≈ 173 (m).

Nhận thấy 9,2 phút < 10 phút nên người đó chèo thuyền từ A thẳng đến điểm D nằm giữa B và C và cách C một đoạn xấp xỉ bằng 173 m, rồi chạy bộ thẳng đến B là phương án tốn ít thời gian nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯