Khám phá trang 15 Chuyên đề Toán 12 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

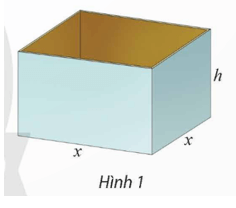
Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là 500 dm (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ 3 dm đến 10 dm.

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu - Chân trời sáng tạo

Khám phá trang 15 Chuyên đề Toán 12: Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là 500 dm³ (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ 3 dm đến 10 dm.

Khám phá trang 15 Chuyên đề Toán 12

a) Nếu gọi độ dài cạnh đáy của thùng là x (dm), chiều cao của thùng là h (dm) thì tổng diện tích các mặt của thùng, kí hiệu S, có thể được biểu thị bằng biểu thức nào?

b) Có thể biểu thị tổng diện tích S theo x không? Biến x nhận giá trị trong miền nào?

c) Với giá trị nào của x thì S có giá trị nhỏ nhất?

Lời giải:

a) Tổng diện tích các mặt của thùng là S = 4xh + x² (dm²).

b) Thể tích của thùng là V = x²h = 500 (dm³).

Suy ra $h = \frac{500}{x^{2}}$ (dm).

Vì 3 ≤ h ≤ 10 nên $3 \leq \frac{500}{x^{2}} \leq 10$ , suy ra $5 \sqrt{2} \leq x \leq \frac{10 \sqrt{15}}{3}$

Khi đó, tổng diện tích các mặt của thùng là

S(x) = $\frac{2000}{x} + x^{2}$ (dm²) với $x \in [5 \sqrt{2}; \frac{10 \sqrt{15}}{3}]$ .

c) Xét hàm số S(x) = $\frac{2000}{x} + x^{2}$ (dm²) với $x \in [5 \sqrt{2}; \frac{10 \sqrt{15}}{3}]$

Ta có S'(x) = $\frac{- 2000}{x^{2}} + 2 x$ ;

Trên khoảng $(5 \sqrt{2}; \frac{10 \sqrt{15}}{3})$ , S'(x) = 0 ⇔ x = 10.

Có $S (5 \sqrt{2}) = 200 \sqrt{2} + 50$ ; S(10) = 300; $S (\frac{10 \sqrt{15}}{3}) = 40 \sqrt{15} + \frac{500}{3}$ .

Do đó, $\min_{[5 \sqrt{2}; \frac{10 \sqrt{15}}{3}]} S (x) = 300$ tại x = 10.

Vậy với x = 10 dm thì S có giá trị nhỏ nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯