Bài 4 trang 21 Chuyên đề Toán 12 Chân trời sáng tạo

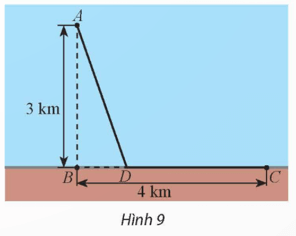
Một giếng dầu ngoài khơi được đặt ở vị trí A cách bờ biển 3 km, B là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí C trên bờ biển, cách vị trí B một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng AD và DC (D là một vị trí nằm giữa B và C). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của D như thế nào để giảm thiểu chi phí lắp đặt nhất?

Giải Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu - Chân trời sáng tạo

Bài 4 trang 21 Chuyên đề Toán 12: Một giếng dầu ngoài khơi được đặt ở vị trí A cách bờ biển 3 km, B là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí C trên bờ biển, cách vị trí B một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng AD và DC (D là một vị trí nằm giữa B và C). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của D như thế nào để giảm thiểu chi phí lắp đặt nhất?

Lời giải:

Đặt BD = x (km, 0 ≤ x ≤ 4).

Ta có DC = 4 – x (km).

Áp dụng định lí Pythagore trong tam giác vuông ABD, ta có:

AD = $\sqrt{x^2+3^2}=\sqrt{x^2+9}$(km).

Giả sử chi phí lắp đặt mỗi mét đường ống dẫn dầu trên bờ là a (đồng, a > 0).

Khi đó chi phí lắp đặt mỗi mét đường ống dẫn dầu đặt dưới biển là 2a (đồng).

Tổng chi phí lắp đặt đường ống là

C = 2a$\sqrt{x^2+9}$ + a(4 – x) = 2a$\sqrt{x^2+9}$ + 4a – ax (đồng).

Xét hàm số f(x) = 2a$\sqrt{x^2+9}$ + 4a – ax với x ∈ [0; 4] và a > 0.

Ta có f'(x) = $\frac{2ax}{\sqrt{x^2+9}}-a$;

          f'(x) = 0 $\iff \frac{2ax}{\sqrt{x^2+9}}-a=0\iff \sqrt{x^2+9}=2x$

     ⇔ x² + 9 = 4x² ⇔ 3x² = 9 ⇔ x² = 3 ⇔ x = $\sqrt{3}$ ∈ [0; 4].

Ta có f(0) = 10a; $f\left(\sqrt{3}\right)=\left(3\sqrt{3}+4\right)a$; f(4) = 10a.

Do đó, $\underset{\left[0;4\right]}{\min }f\left(x\right)=f\left(\sqrt{3}\right)=\left(3\sqrt{3}+4\right)a$(do a > 0) tại x = $\sqrt{3}$.

Vậy cần đặt vị trí D nằm giữa B và C sao cho D cách B một khoảng bằng $\sqrt{3}$km để giảm thiểu chi phí lắp đặt nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Vận dụng đạo hàm giải bài toán tối ưu hay, chi tiết khác:

• Khởi động trang 15 Chuyên đề Toán 12: Một người đang ở vị trí A muốn đi đến vị trí B trên bờ hồ như hình bên ....

• Khám phá trang 15 Chuyên đề Toán 12: Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp ....

• Thực hành 1 trang 17 Chuyên đề Toán 12: Hai nhà máy được đặt tại các vị trí A và B cách nhau 4 km ....

• Thực hành 2 trang 18 Chuyên đề Toán 12: Mặt cắt ngang của một máng dẫn nước là một hình thang cân có độ dài ....

• Thực hành 3 trang 19 Chuyên đề Toán 12: Tại một xưởng sản xuất, chi phí để sản xuất x sản phẩm mỗi tháng là ....

• Thực hành 4 trang 20 Chuyên đề Toán 12: Cơ sở A chuyên cung cấp một loại sản phẩm nông nghiệp X cho nhà phân phối B ....

• Vận dụng trang 20 Chuyên đề Toán 12: Hiện tại, mỗi tháng một cửa hàng đồ lưu niệm bán được 100 sản phẩm A ....

• Bài 1 trang 20 Chuyên đề Toán 12: Người ta muốn xây một đường cống thoát nước có mặt cắt ngang ....

• Bài 2 trang 20 Chuyên đề Toán 12: Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1 800 m3 và chiều sâu 2 m ....

• Bài 3 trang 20 Chuyên đề Toán 12: Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước ....

• Bài 5 trang 21 Chuyên đề Toán 12: Tại một xí nghiệp, nếu trong một tuần xí nghiệp sản xuất x nghìn sản phẩm ....