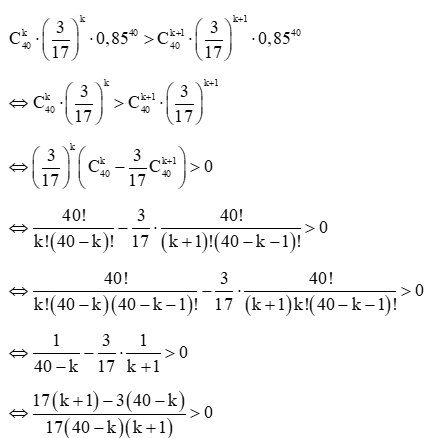Bài 4 trang 70 Chuyên đề Toán 12 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Tỉ lệ phát bóng hỏng của một vận động viên bóng chuyền là 15%. Vận động viên đó thực hiện 40 quả phát bóng một cách độc lập với nhau. Gọi X là số quả phát bóng hỏng trong 40 quả đó.

Giải Chuyên đề Toán 12 Bài 2: Phân bố Bernoulli và phân bố nhị thức - Chân trời sáng tạo

Bài 4 trang 70 Chuyên đề Toán 12: Tỉ lệ phát bóng hỏng của một vận động viên bóng chuyền là 15%. Vận động viên đó thực hiện 40 quả phát bóng một cách độc lập với nhau. Gọi X là số quả phát bóng hỏng trong 40 quả đó.

a) Tính kì vọng và phương sai của X.

b) Hỏi xác suất X nhận giá trị bằng bao nhiêu là lớn nhất?

Lời giải:

Gọi T là phép thử “Vận động viên phát ngẫu nhiên một quả bóng”. Theo đề bài, phép thử T được lặp lại 40 lần một cách độc lập. Gọi A là biến cố “Quả bóng bị phát hỏng”. Ta có P(A) = 15% = 0,15.

Do phép thử T được thực hiện 40 lần một cách độc lập với nhau và xác suất xảy ra biến cố A trong mỗi lần thử đều bằng 0,15 nên X là biến cố ngẫu nhiên rời rạc có phân bố nhị thức B(40; 0,15).

a) Kì vọng của X là: E(X) = np = 40 . 0,15 = 6.

Phương sai của X là: V(X) = np(1 – p) = 40 . 0,15 . (1 – 0,15) = 5,1.

b) Ta có:

$P (X = k) = C_{40}^{k} \cdot 0, 15^{k} \cdot {(1 - 0, 15)}^{40 - k}$ (với k = 0, 1, …, 40)

$= C_{40}^{k} \cdot 0, 15^{k} \cdot 0, 85^{40 - k} = C_{40}^{k} \cdot {(\frac{0, 15}{0, 85})}^{k} \cdot 0, 85^{40} = C_{40}^{k} \cdot {(\frac{3}{17})}^{k} \cdot 0, 85^{40} .$

Khi đó: $P (X = k + 1) = C_{40}^{k + 1} \cdot {(\frac{3}{17})}^{k + 1} \cdot 0, 85^{40}$ với k = 0, 1, …, 39.

⦁ Trường hợp 1. Nếu P(X = k) > P(X = k + 1) thì ta có:

Bài 4 trang 70 Chuyên đề Toán 12 Chân trời sáng tạo

⇔ 17k + 17 – 120 + 3k > 0 (do 40 – k > 0)

⇔ 20k > 103

$\Leftrightarrow k > \frac{103}{20} = 5, 15$

Mà k ∈ {0; 1; …; 40} nên k ∈ {6; 7; …; 50}.

Khi đó P(X = 6) > P(X = 7) > … > P(X = 40).

⦁ Trường hợp 2. Nếu P(X = k) < P(X = k + 1) thì tương tự trường hợp 1, ta có: k < 5,15.

Mà k ∈ {0; 1; …; 39} nên k ∈ {0; 1; ..; 5}.

Khi đó P(X = 0) < P(X = 1) < … < P(X = 5).

⦁ Xét $P (X = 5) = C_{40}^{5} \cdot {(\frac{3}{17})}^{5} \cdot 0, 85^{40} \approx 0, 169;$

$P (X = 6) = C_{40}^{6} \cdot {(\frac{3}{17})}^{6} \cdot 0, 85^{40} \approx 0, 174.$

Do đó P(X = 5) < P(X = 6).

Suy ra P(X = 0) < P(X = 1) < … < P(X = 5) < P(X = 6) > P(X = 7) > … > P(X = 40).

Vì vậy, P(X = 6) có giá trị lớn nhất.

Vậy xác suất X nhận giá trị bằng 6 là lớn nhất.

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Phân bố Bernoulli và phân bố nhị thức hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯