Thực hành 5 trang 70 Chuyên đề Toán 12 Chân trời sáng tạo

Cho biến ngẫu nhiên rời rạc X có phân bố nhị thức B(5; 0,2).

Giải Chuyên đề Toán 12 Bài 2: Phân bố Bernoulli và phân bố nhị thức - Chân trời sáng tạo

Thực hành 5 trang 70 Chuyên đề Toán 12: Cho biến ngẫu nhiên rời rạc X có phân bố nhị thức B(5; 0,2).

a) Tính xác suất của biến cố “X lớn hơn 3”.

b) Tính kì vọng và độ lệch chuẩn của X.

Lời giải:

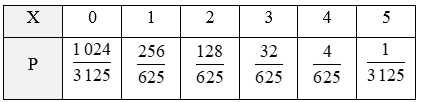
Ta có $P\left(X=k\right)=C_5^k\cdot 0,2^k\cdot {\left(1-0,2\right)}^{5-k}=C_5^k\cdot 0,2^k\cdot 0,8^{5-k},$ với k = 0, 1, 2, 3, 4, 5.

Lần lượt tính P(X = k) với k = 0, 1, 2, 3, 4, 5 từ công thức trên, ta thu được bảng phân bố xác suất của X như sau:

a) Xác suất của biến cố “X lớn hơn 3” là:

$P\left(X>3\right)=P\left(X=4\right)+P\left(X=5\right)=\frac{4}{625}+\frac{1}{3125}=\frac{21}{3125}.$

b) Kì vọng của X là:

$E\left(X\right)=0\cdot \frac{1024}{3125}+1\cdot \frac{256}{625}+2\cdot \frac{128}{625}+3\cdot \frac{32}{625}+4\cdot \frac{4}{625}+5\cdot \frac{1}{3125}=1.$

Phương sai của X là:

$V\left(X\right)=0^2\cdot \frac{1024}{3125}+1^2\cdot \frac{256}{625}+2^2\cdot \frac{128}{625}+3^2\cdot \frac{32}{625}+4^2\cdot \frac{4}{625}+5^2\cdot \frac{1}{3125}-1^2=\frac{4}{5}.$

Độ lệch chuẩn của X là:

$\sigma \left(X\right)=\sqrt{V\left(X\right)}=\sqrt{\frac{4}{5}}=\frac{2\sqrt{5}}{5}.$

Chú ý: Ta cũng có thể tính kì vọng và phương sai của X như sau:

E(X) = np = 5 . 0,2 = 1 và V(X) = np(1 – p) = 5 . 0,2 . (1 – 0,2) = 0,8.

Do đó độ lệch chuẩn của X là: $\sigma \left(X\right)=\sqrt{V\left(X\right)}=\sqrt{0,8}=\frac{2\sqrt{5}}{5}.$

Lời giải bài tập Chuyên đề Toán 12 Bài 2: Phân bố Bernoulli và phân bố nhị thức hay, chi tiết khác:

• Khởi động trang 64 Chuyên đề Toán 12: Một loại hạt giống có xác suất nảy mầm là 0,9. Bác Hoan gieo 100 hạt giống đó một cách độc lập với nhau...

• Khám phá 1 trang 64 Chuyên đề Toán 12: Thuyền trưởng Vinh gửi một tín hiệu vô tuyến từ thuyền đến trạm điều khiển....

• Thực hành 1 trang 65 Chuyên đề Toán 12: Trong các biến ngẫu nhiên rời rạc sau, biến ngẫu nhiên rời rạc nào có phân bố Bernoulli? ....

• Khám phá 2 trang 66 Chuyên đề Toán 12: Xét phép thử ngẫu nhiên T là “Gieo một đồng xu cân đối và đồng chất”. Hãy liệt kê tất cả các kết quả có thể xảy ....

• Thực hành 2 trang 67 Chuyên đề Toán 12: Trong Hoạt động khởi động (trang 64), hãy tính xác suất của biến cố “Trong 100 hạt giống bác Hoan gieo, có đúng 90 hạt nảy mầm”.....

• Thực hành 3 trang 67 Chuyên đề Toán 12: Tỉ lệ người lao động có bằng đại học ở một khu công nghiệp là 30%. Tiến hành phỏng vấn lần lượt 10 người lao động ....

• Khám phá 3 trang 67 Chuyên đề Toán 12: Một công ty dược nhận thấy xác suất một bệnh nhân có phản ứng phụ khi được điều trị bằng một loại thuốc M là 0,08....

• Thực hành 4 trang 70 Chuyên đề Toán 12: Tính kì vọng của X ở Hoạt động khám phá 3 (trang 67).....

• Vận dụng trang 70 Chuyên đề Toán 12: Vào đầu mùa đông, trang trại A lắp mới 10 bóng đèn để sưởi ấm cho gà. Các bóng đèn hoạt động độc lập với nhau ....

• Bài 1 trang 70 Chuyên đề Toán 12: Một hộp chứa 10 tấm thẻ cùng loại được đánh số từ 1 đến 10. Trong các biến ngẫu nhiên rời rạc dưới đây...

• Bài 2 trang 70 Chuyên đề Toán 12: Tỉ lệ người có nhóm máu O trong một cộng đồng là 40%. Chọn ngẫu nhiên một cách độc lập 8 người từ cộng đồng đó.....

• Bài 3 trang 70 Chuyên đề Toán 12: Có 60% tài xế thường xuyên nghe tin tức giao thông trên đài khi lái xe. Chọn ngẫu nhiên một cách độc lập 6 tài xế....

• Bài 4 trang 70 Chuyên đề Toán 12: Tỉ lệ phát bóng hỏng của một vận động viên bóng chuyền là 15%. Vận động viên đó thực hiện 40 quả phát bóng ....