Thực hành 4 trang 60 Chuyên đề Toán 12 Chân trời sáng tạo

Một hộp chứa 3 tấm thẻ cùng loại được đánh số từ 1 đến 3.

Giải Chuyên đề Toán 12 Bài 1: Biến ngẫu nhiên rời rạc - Chân trời sáng tạo

Thực hành 4 trang 60 Chuyên đề Toán 12: Một hộp chứa 3 tấm thẻ cùng loại được đánh số từ 1 đến 3.

a) Lấy ra ngẫu nhiên 1 thẻ từ hộp. Gọi X là số ghi trên thẻ đó. Hãy tính kì vọng của X.

b) Lấy ra ngẫu nhiên đồng thời 2 thẻ từ hộp. Gọi Y là số lớn hơn trong hai số ghi trên hai thẻ đó. Hãy tính kì vọng của Y.

Lời giải:

a) X là biến cố ngẫu nhiên rời rạc và nhận các giá trị trong tập hợp {1; 2; 3}.

Tổng số kết quả có thể xảy ra khi chọn ngẫu nhiên 1 thẻ từ hộp là: n(Ω) = 3.

Do chỉ có 1 tấm thẻ được đánh số 1 nên số kết quả thuận lợi cho biến cố “X bằng 1” là 1. Vậy xác suất của biến cố “X = 1” là: $P (X = 1) = \frac{1}{3} .$

Tương tự, ta có $P (X = 2) = \frac{1}{3};$ $P (X = 3) = \frac{1}{3} .$

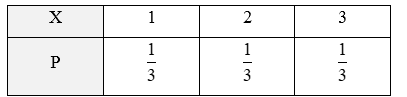
Bảng phân bố xác suất của X là:

Thực hành 4 trang 60 Chuyên đề Toán 12 Chân trời sáng tạo

Kì vọng của X là:

$E (X) = 0 \cdot \frac{1}{3} + 2 \cdot \frac{1}{3} + 3 \cdot \frac{1}{3} = \frac{5}{3} .$

b) Y là biến cố ngẫu nhiên rời rạc và nhận các giá trị trong tập hợp {2; 3}.

Tổng số kết quả có thể xảy ra khi chọn ngẫu nhiên đồng thời 2 thẻ từ hộp là: n(Ω) = 3.

Do chỉ có một trường hợp xảy ra mà số lớn hơn trong hai số ghi trên hai thẻ đó là 2 (một thẻ ghi số 1 và một thẻ ghi số 2) nên số kết quả thuận lợi cho biến cố “Y bằng 2” là 1.

Xác suất của biến cố “Y = 2” là: $P (Y = 2) = \frac{1}{3} .$

Tương tự, ta có $P (Y = 3) = \frac{2}{3} .$

Bảng phân bố xác suất của Y là:

Y	2	3
P	$\frac{1}{3}$	$\frac{2}{3}$

Kì vọng của Y là:

$E (Y) = 2 \cdot \frac{1}{3} + 3 \cdot \frac{2}{3} = \frac{8}{3} .$

Lời giải bài tập Chuyên đề Toán 12 Bài 1: Biến ngẫu nhiên rời rạc hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯