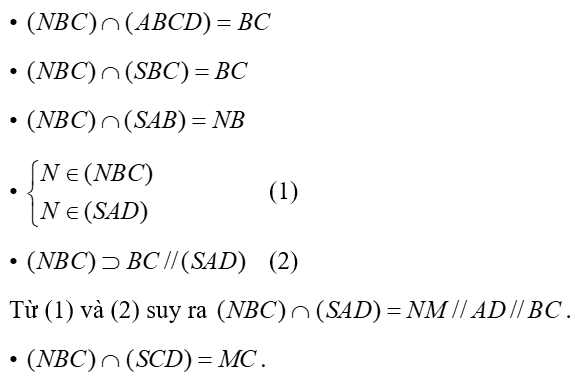Đề thi Giữa kì 1 Toán 11 Chân trời sáng tạo có đáp án (10 đề + ma trận)

---

Haylamdo biên soạn và sưu tầm bộ 10 Đề thi Toán 11 Giữa kì 1 Chân trời sáng tạo năm 2024 có đáp án và ma trận được biên soạn và chọn lọc bám sát chương trình sách mới từ đề thi Toán 11 của các trường THPT trên cả nước sẽ giúp học sinh lớp 11 ôn tập và đạt kết quả cao trong các bài thi Giữa học kì 1 Toán 11.

Đề thi Giữa kì 1 Toán 11 Chân trời sáng tạo có đáp án (10 đề + ma trận)

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Chân trời sáng tạo

Năm học 2023 - 2024

Môn: Toán lớp 11

Thời gian làm bài: phút

(Đề số 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây.

Câu 1. Đổi số đo của góc $\alpha =30°$ sang rađian.

A. $\alpha =\frac{\pi }{2}.$

B. $\alpha =\frac{\pi }{4}.$

C. $\alpha =\frac{\pi }{6}.$

D. $\alpha =\frac{\pi }{3}.$

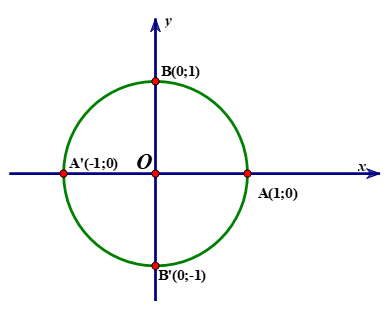
Câu 2. Trong mặt phẳng tọa độ $Oxy,$cho đường tròn lượng giác như hình vẽ bên dưới. Hỏi góc lượng giác nào sau đây có số đo là $90°?$

A. $\left(OA,O{B}^{\text{'}}\right).$

B. $\left(OA,OA\right).$

C. $\left(OA,OB\right).$

D. $\left(OA,O{A}^{\text{'}}\right).$

Câu 3. Trong mặt phẳng tọa độ $Oxy,$ trên đường tròn lượng giác gọi điểm M là điểm biểu diễn của góc $\alpha =\frac{\pi }{6}.$ Lấy điểm N đối xứng với M qua gốc tọa độ. Hỏi N là điểm biểu diễn của góc có số đo bằng bao nhiêu?

A. $\frac{7\pi }{6}.$

B. $\frac{5\pi }{6}.$

C. $-\frac{\pi }{6}.$

D. $\frac{4\pi }{3}.$

Câu 4. Cho $\alpha$ thuộc góc phần phần tư thứ nhất của đường tròn lượng giác. Khẳng định nào sau đây là đúng?

A. $\sin \alpha >0$

B. $\cos \alpha <0$.

C. $\tan \alpha <0$.

D. $\cot \alpha <0$.

Câu 5. Mệnh đề nào sau đây là sai?

A. $-1\le \sin \alpha \le 1;-1\le \cos \alpha \le 1$.

B. $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }(\cos \alpha \ne 0)$.

C. $\tan \alpha =\frac{\cos \alpha }{\sin \alpha }(\sin \alpha \ne 0)$.

D. ${\sin }^2\left(2024\alpha \right)+{\cos }^2\left(2024\alpha \right)=2024$.

Câu 6.Cho góc $\alpha$ thỏa mãn $\cos \alpha =-\frac{\sqrt{5}}{3}$ và $\pi <\alpha <\frac{3\pi }{2}$. Tính $\tan \alpha$.

A. $\tan \alpha =-\frac{3}{\sqrt{5}}$.

B. $\tan \alpha =\frac{2}{\sqrt{5}}$.

C. $\tan \alpha =-\frac{4}{\sqrt{5}}$.

D. $\tan \alpha =-\frac{2}{\sqrt{5}}.$

Câu 7.Khẳng định nào sau đây đúng?

A. $\sin \left(2024a\right)=2024\sin a\cos a$.

B. $\sin \left(2024a\right)=2024\sin \left(1012a\right)\cos \left(1012a\right)$.

C. $\sin \left(2024a\right)=2\sin a\cos a$.

D. $\sin \left(2024a\right)=2\sin \left(1012a\right)\cos \left(1012a\right)$

Câu 8.Cho các đẳng thức sau:

1) $\cos x-\sin x=\sqrt{2}\sin \left(x+\frac{\pi }{4}\right)$.

2) $\cos x-\sin x=\sqrt{2}\cos \left(x+\frac{\pi }{4}\right)$.

3) $\cos x-\sin x=\sqrt{2}\cos \left(x-\frac{\pi }{4}\right)$.

4) $\cos x-\sin x=\sqrt{2}\sin \left(\frac{\pi }{4}-x\right)$.

Có bao nhiêu đẳng thức dưới đây là đồng nhất thức?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 9. Cho góc $\alpha$ thỏa mãn $\cos 2\alpha =\frac{2}{3}$. Tính $P={\sin }^4\alpha +{\cos }^4\alpha$.

A. $P=1$.

B. $P=\frac{17}{81}$.

C. $P=\frac{7}{9}$.

D. $P=\frac{9}{7}$.

Câu 10. Tìm tập xác định D của hàm số $y=\frac{1+\sin x}{\cos x-1}.$

A. $\text{D}=ℝ.$

B. $\text{D}=ℝ\backslash \left(\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right).$

C. $\text{D}=ℝ\backslash \left(k\pi ,k\in \mathbb{Z}\right).$

D. $\text{D}=ℝ\backslash \left(k2\pi ,k\in \mathbb{Z}\right).$

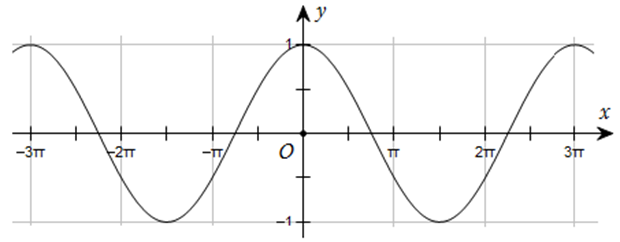
Câu 11. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

Hỏi hàm số đó là hàm số nào?

A. $y=\cos \frac{2x}{3}.$

B. $y=\sin \frac{2x}{3}.$

C. $y=\cos \frac{3x}{2}.$

D. $y=\sin \frac{3x}{2}.$

Câu 12. Hàm số $y=5+4\sin 2x\cos 2x$ có tất cả bao nhiêu giá trị nguyên?

A. 3.

B. 4.

C. 5.

D. 6.

Câu 13. Trong các phương trình sau, phương trình tương đương với phương trình $x^2-1=0$ là

A. $x-1=0$.

B. $2x^2=2$.

C. $x^2-2=0$.

D. $x^2+1=0$.

Câu 14. Tất cả nghiệm của phương trình $\cos x=-\frac{\sqrt{3}}{2}$ là

A. $x=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

B. $x=\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

C. $x=\pm \frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

D. $x=\pm \frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

Câu 15. Tất cả nghiệm của phương trình $\tan \left(30°-3x\right)=\tan 75°$ là

A. $x=45°+k180°,k\in \mathbb{Z}$.

B. $x=-15°+k60°,k\in \mathbb{Z}$.

C. $x=-15°+k180°,k\in \mathbb{Z}$.

D. $x=-15°-k60°,k\in \mathbb{Z}$

Câu 16. Nghiệm âm lớn nhất của phương trình lượng giác $\cos 2x=\cos \left(x+\frac{\pi }{3}\right)$ là

A. $-\frac{\pi }{9}$.

B. $-\frac{5\pi }{3}$

C. $-\frac{7\pi }{9}$.

D. $-\frac{13\pi }{9}$.

Câu 17. Cho dãy số $\left(u_n\right)$ là dãy số tự nhiên lẻ theo thứ tự tăng dần và $u_1=3$. Năm số hạng đầu của dãy số $\left(u_n\right)$ là:

A. $1;3;5;7;9$.

B. $1;2;3;4;5$.

C. $3;5;7;9;11$.

D. $0;1;3;5;7.$

Câu 18. Trong các dãy số sau, dãy số nào không là dãy số bị chặn?

A.$\left(a_n\right)$ với $a_n=3^n$.

B. $\left(u_n\right)$ với $u_n=\sin \left(n\frac{\pi }{2}\right)$

C.$\left(b_n\right):2;4;6;8;10$

D.$\left(v_n\right)$ với $v_n=\frac{1}{n+1}$.

Câu 19. Cho dãy số$\left(u_n\right)$ với $u_n=\frac{n+a}{n}$, a là số thực. Tìm một giá trị của a để $\left(u_n\right)$ là dãy số giảm.

A. $-\frac{1}{2}$.

B. 1.

C. 0.

D. $a=-1$.

Câu 20. Trong các dãy số được cho dưới đây, dãy số nào không phải là cấp số cộng?

A.$u_n=-4n+9$.

B.$u_n=-2n+19$.

C.$u_n=-2n-21$.

D.$u_n=-2^n+15$.

Câu 21. Trong các dãy số được cho dưới đây, dãy số nào không phải là cấp số cộng?

A. $u_n=7-3n$.

B. $u_n=7-3^n$.

C. $u_n=\frac{7}{3^n}$.

D. $u_n=7.3^n$.

Câu 22. Cho hai số -3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành cấp số cộng có công sai d=2. Tìm n.

A. n=12

B. n=13.

C. n=14.

D. n=15.

Câu 23. T$2x-1;x;2x+1$ìm n số hạng đầu tiên của một cấp số cộng $S_n=n^2+4n$ với $n\in \mathbb{N}*$. Tìm số hạng tổng quát $u_n$ của cấp số cộng đã cho.

A.$u_n=2n+3$.

B.$u_n=3n+2$.

C.$u_n=5.3^{n-1}$.

D.$u_n=5.{\left(\frac{8}{5}\right)}^{n-1}.$

Câu 24. Dãy số nào sau đây không phải là cấp số nhân?

A. $2;4;8;16;\mathrm{...}$

B.$1;-1;1;-1;\mathrm{...}$

C. $1^2;2^2;3^2;4^2;\mathrm{...}$.

D.$a;a^3;a^5;a^7;\mathrm{...}(a\ne 0)$

Câu 25. Dãy số $1;2;4;8;16;32;\mathrm{...}$ là cấp số nhânvới

A. Công bội là 3 và số hạng đầu tiên là 1.

B.Công bội là 2 và số hạng đầu tiên là 1.

C.Công bội là 4 và số hạng đầu tiên là 2.

D.Công bội là 2 và số hạng đầu tiên là 2.

Câu 26. Tìm tất cả giá trị của $x$ để ba số $2x-1;x;2x+1$ theo thứ tự đó lập thành một cấp số nhân.

A.$x=\pm \frac{1}{\sqrt{3}}$.

B.$x=\pm \frac{1}{3}$.

C.$x=\pm \sqrt{3}$.

D.$x=\pm 3$

Câu 27. Cho cấp số nhân $\left(u_n\right)$ có tổng n số hạng đầu tiên là $S_n=\frac{3^n-1}{3^{n-1}}$. Tìm số hạng thứ 5 của cấp số nhân đã cho.

A.$u_5=\frac{2}{3^4}$ .

B.$u_5=\frac{1}{3^5}$.

C.$u_5=3^5$

D.$u_5=\frac{5}{3^5}$.

Câu 28. Trong các khẳng định sau, khẳng định nào đúng?

A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng.

B.Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.

C.Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.

D.Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.

Câu 29. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?

A. Ba điểm phân biệt.

B.Một điểm và một đường thẳng.

C.Hai đường thẳng cắt nhau.

D.Bốn điểm phân biệt.

Câu 30. Cho mặt phẳng $\left(\alpha \right)$, cho 4 điểm $A,B,C,D$ trong đó không có ba điểm nào thẳng hàng. Điểm S không thuộc mặt phẳng $\left(\alpha \right)$. Có mấy mặt phẳng tạo bởi S và 2 trong 4 điểm nói trên?

A.4.

B.8.

C.5.

D.6.

Câu 31. Cho bốn điểm $A,B,C,D$ không đồng phẳng. Gọi $M,N$ lần lượt là trung điểm của $AC$ và $BC$. Trên đoạn $BD$ lấy điểm P sao cho $BP=2PD$. Giao điểm của đường thẳng $CD$ và mặt phẳng $\left(MNP\right)$ là giao điểm của

A. CD và NP.

B. CD và MN.

C. CD và MP.

D.CD và AP.

Câu 32. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác.

B.Hai đường thẳng song song khi và chỉ khi chúng không có điểm chung.

C.Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.

D.Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.

Câu 33. Trong không gian, cho ba đường thẳng phân biệt $a,b,c$ trong đó $a\text{//}b$. Khẳng định nào sau đây sai?

A. Nếu $a\text{//}b$ thì $b\text{//}c$.

B.Nếu c cắt a thì c cắt b.

C.Nếu $A\in a$ và $B\in b$ thì ba đường thẳng $a,b,AB$ cùng ở trên một mặt phẳng.

D.Tồn tại duy nhất một mặt phẳng qua a và b.

Câu 34. Cho hình chóp $S.ABCD$ có $ABCD$ là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng $\left(SAD\right)$ và $\left(SBC\right)$. Khẳng định nào sau đây đúng?

A. d qua S và song song với BC.

B. d qua S và song song với DC.

C. d qua S và song song với AB.

D. d qua S và song song với BD.

Câu 35. Gọi G là trọng tâm tứ diện $ABCD$. Gọi $A^{\text{'}}$ là trọng tâm của tam giác $BCD$. Tính tỉ số $\frac{GA}{G{A}^{\text{'}}}$

A.2.

B.3.

C.$\frac{1}{3}$

D.$\frac{1}{2}$

II. Tự luận (3,0 điểm)

Bài 1. (1,0 điểm) Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số $y=4\sin \left(\frac{\pi }{178}\left(t-60\right)\right)+10$ với $t\in \mathbb{Z}$ và $0<t\le 365$. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?

Bài 2. (1,0 điểm) Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau đặt gấp đôi lần cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khách trên thắng hay thua bao nhiêu?

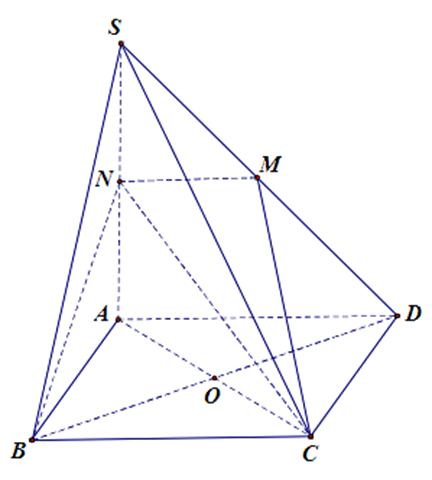
Bài 3. (1,0 điểm) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành và N là trung điểm của cạnh SA.

a) Tìm giao điểm của AC và mặt phẳng (SBD)

b) Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (NBC). Thiết diện là hình gì?

-------------- HẾT --------------

ĐÁP ÁN ĐỀ SỐ 01

I. Bảng đáp án trắc nghiệm

1. C	2. C	3. A	4. A	5. D	6. B	7. D
8. B	9. C	10. D	11. A	12. C	13. B	14. D
15. D	16. A	17. C	18. D	19. B	20. D	21. A
22. A	23. A	24. C	25. B	26. A	27. A	28. C
29. C	30. D	31. A	32. D	33. B	34. A	35. B

II. Hướng dẫn giải chi tiết tự luận

Bài 1. (1,0 điểm)

Mà $k\in \mathbb{Z}$ nên $k=0$.

Với k = 0 rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện $0<t\le 365$ thì ta biết năm này tháng 2 chỉ có 28 ngày).

Bài 2. (1,0 điểm)

Du khách thu trong 9 lần đầu tiên nên tổng số tiền thua là:

S₉ = u₁ + u₂ + ... + u₉ = $\frac{u_1\left(1-p^9\right)}{1-p}$ = 10 220 000 (đồng)

Số tiền mà du khách thắng trong lần thứ 10 là:

u₁₀ = u₁p⁹ = 10 240 000 (đồng)

Ta có u₁₀ - S₉ = 10 240 000 - 10 220 000 = 20 000 > 0 nên du khách thắng 20 000 đồng.

Bài 3. (1,0 điểm)

a) Gọi O là giao điểm của AC và BD.

Khi đó $\left\{\begin{array}{l}O\in AC\\ O\in ND\subset \left(SBD\right)\end{array}\right.$.

Vậy O là giao điểm của AC và mặt phẳng (SBD).

b) Ta có:

Vậy thiết diện là hình thang MNCD.

................................

................................

................................

Trên đây tóm tắt một số nội dung có trong bộ Đề thi Toán 11 Chân trời sáng tạo năm 2024 mới nhất, để mua tài liệu đầy đủ, Thầy/Cô vui lòng truy cập tailieugiaovien.com.vn

Tham khảo đề thi Toán 11 Chân trời sáng tạo có đáp án hay khác:

• Đề thi Học kì 1 Toán 11 Chân trời sáng tạo (có đáp án)

• Đề thi Giữa kì 2 Toán 11 Chân trời sáng tạo (có đáp án)

• Đề thi Học kì 2 Toán 11 Chân trời sáng tạo (có đáp án)

Xem thêm đề thi lớp 11 Chân trời sáng tạo có đáp án hay khác: