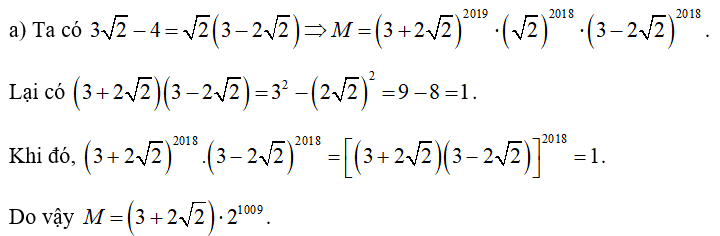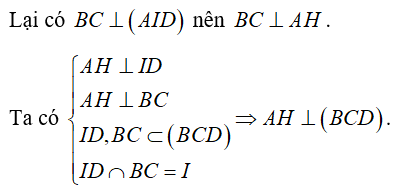Đề thi Giữa kì 2 Toán 11 Chân trời sáng tạo có đáp án (10 đề + ma trận)

---

Haylamdo biên soạn và sưu tầm bộ 10 Đề thi Toán 11 Giữa kì 2 Chân trời sáng tạo năm 2024 có đáp án và ma trận được biên soạn và chọn lọc bám sát chương trình sách mới từ đề thi Toán 11 của các trường THPT trên cả nước sẽ giúp học sinh lớp 11 ôn tập và đạt kết quả cao trong các bài thi Giữa học kì 2 Toán 11.

Đề thi Giữa kì 2 Toán 11 Chân trời sáng tạo có đáp án (10 đề + ma trận)

Xem thử

Chỉ từ 150k mua trọn bộ Đề thi Giữa kì 2 Toán 11 Chân trời sáng tạo bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Sở Giáo dục và Đào tạo ...

Đề thi Giữa kì 2 - Chân trời sáng tạo

Năm học 2023 - 2024

Môn: Toán lớp 11

Thời gian làm bài: phút

(Đề số 1)

I. Trắc nghiệm (7 điểm)

Câu 1. Cho a là số thực dương. Với n thuộc tập hợp nào thì khẳng định $a^n=\underset{n}{\underbrace{a.a\mathrm{............}a}}$ đúng?

A. n ∈ ℝ.

B. n ∈ ℤ.

C. n ∈ ℕ.

D. n ∈ ℕ*.

Câu 2. Với a là số thực dương tùy ý, $\sqrt{a^3}$ bằng kết quả nào sau đây?

A. a⁶.

B. $a^{\frac{3}{2}}$.

C. $a^{\frac{2}{3}}$.

D. $a^{\frac{1}{6}}$.

Câu 3. Với α là số thực bất kì, mệnh đề nào sau đây sai?

A. $\sqrt{{10}^{\alpha }}={\left(\sqrt{10}\right)}^{\alpha }$.

B. $\sqrt{{10}^{\alpha }}={10}^{\frac{\alpha }{2}}$.

C. ${\left({10}^{\alpha }\right)}^2={\left(100\right)}^{\alpha }$.

D. ${\left({10}^{\alpha }\right)}^2={\left(10\right)}^{{\alpha }^2}$.

Câu 4. Cho đẳng thức $\frac{\sqrt[3]{a^2\sqrt{a}}}{a^3}=a^{\alpha }\mathrm{,0}<a\ne 1$. Khi đó α thuộc khoảng nào sau đây?

A. (-2; -1).

B. (-1; 0).

C. (-3; -2).

D. (0; 1).

Câu 5. Chị Hà gửi vào ngân hàng 20 000 000 đồng với lãi suất 0,5%/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau 1 năm chị Hà nhận được bao nhiêu tiền, biết trong 1 năm đó chị Hà không rút tiền lần nào và lãi suất không thay đổi (làm tròn đến hàng nghìn).

A. 21 233 000 đồng.

B. 21 235 000 đồng.

C. 21 234 000 đồng.

D. 21 200 000 đồng.

Câu 6. Với điều kiện nào của a, b thì khẳng định ${\log }_{a}b=\alpha \iff a^{\alpha }=b$ là đúng?

A. a, b > 0, a ≠ 1.

B. a, b > 0.

C. a > 0, a ≠ 1.

D. b > 0, a ≠ 1.

Câu 7. Trong các mệnh đề sau, mệnh đề nào đúng?

A. ${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$ với mọi số thực dương a, b và a ≠ 1.

B. ${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$ với mọi số thực dương a, b.

C. ${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$ với mọi số thực a, b.

D. ${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$ với mọi số thực a, b và a ≠ 1.

Câu 8. Với a là số thực dương tùy ý, ${\log }_3\left(9a\right)$ bằng

A. $\frac{1}{2}+{\log }_{3}a$.

B. $2{\log }_{3}a$.

C. ${\left({\log }_{3}a\right)}^2$.

D. $2+{\log }_{3}a$.

Câu 9. Cho 0 < a ≠ 1. Giá trị của biểu thức $P={\log }_a\left(a\cdot \sqrt[3]{a^2}\right)$ là

A. $\frac{4}{3}$.

B. 3.

C. $\frac{5}{3}$.

D. $\frac{5}{2}$.

Câu 10. Cho a, b, c là các số thực dương thỏa mãn a² = bc. Giá trị của biểu thức $S=2\ln a-\ln b-\ln c$ là

A. $S=2\ln \left(\frac{a}{bc}\right)$.

B. S = 1.

C. $S=-2\ln \left(\frac{a}{bc}\right)$.

D. S = 0.

Câu 11. Hàm số nào dưới đây là hàm số mũ?

A. $y=x^{\sqrt{3}}$.

B. $y=x^{\log 2}$.

C. $y={\log }_{\sqrt{2}}x$.

D. $y={\left(\frac{\pi }{3}\right)}^x$.

Câu 12. Cho các hàm số sau:

$y={\log }_{2}x$, $y={\log }_{\sqrt{3}}x$, $y=\ln x$, $y={\log }_{2^{-3}}x$, $y={\log }_{x}5$.

Có bao nhiêu hàm số lôgarit trong các hàm số trên?

A. 5.

B. 4.

C. 3.

D. 2.

Câu 13. Tập xác định của hàm số $y={\log }_{2}x$ là

A. $\left[0;+\infty \right)$.

B. $\left(-\infty ;+\infty \right)$.

C. $\left(0;+\infty \right)$.

D. $\left[2;+\infty \right)$.

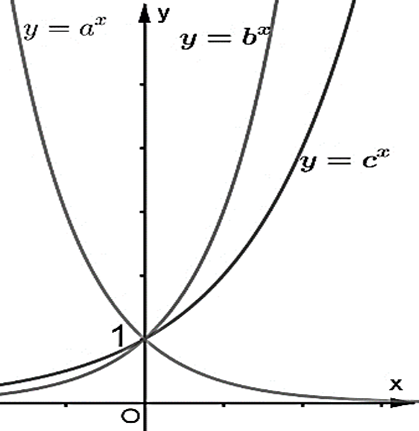
Câu 14. Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số $y=a^x,y=b^x,y=c^x$ được cho trong hình vẽ sau.

Mệnh đề nào dưới đây đúng?

A. b < c < a.

B. c < a < b.

C. a < b < c.

D. a < c < b.

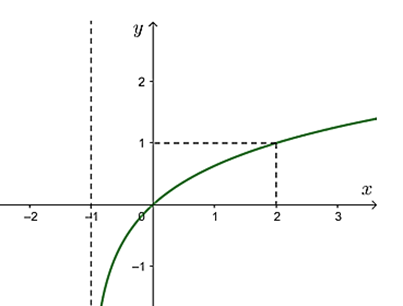
Câu 15. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. $y={\log }_{2}x$. B. $y={\log }_2\left(x+1\right)$. C. $y={\log }_{3}x+1$. D. $y={\log }_3\left(x+1\right)$.

Câu 16. Nghiệm của phương trình 7^x = 2 là

A. $x={\log }_{7}2$.

B. $x={\log }_{2}7$.

C. $x=\frac{2}{7}$.

D. $x=\sqrt{7}$.

Câu 17. Nghiệm của phương trình ${\log }_3\left(5x\right)=2$ là

A. $x=\frac{8}{5}$.

B. x = 9.

C. $x=\frac{9}{5}$.

D. x = 8.

Câu 18. Tập nghiệm của bất phương trình ${\log }_{\frac{2}{3}}\left(x-2\right)\ge 1$ là

A. $\left[\frac{8}{3};+\infty \right)$.

B. $\left[2;\frac{8}{3}\right]$.

C. $\left(2;\frac{8}{3}\right]$.

D. $\left(-\infty ;\frac{8}{3}\right]$.

Câu 19. Tập nghiệm của bất phương trình $2^{x-3}>16$ là

A. $\left[7;+\infty \right)$.

B. $\left(0;+\infty \right)$.

C. $\left(7;+\infty \right)$.

D. $\left(3;+\infty \right)$.

Câu 20. Biết phương trình $4^x-9\cdot 2^x+16=0$ có hai nghiệm phân biệt x₁, x₂. Tính giá trị của biểu thức A = x₁ + x₂.

A. A = 4.

B. A = ${\log }_{2}9$.

C. A = 9.

D. A = 16.

Câu 21. Trong không gian cho hai đường thẳng thẳng m và n. Phát biểu nào sau đây là đúng?

A. Góc giữa hai đường thẳng m và n là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.

B. Góc giữa hai đường thẳng m và n là góc giữa hai đường thẳng m và b vuông góc với n.

C. Góc giữa hai đường thẳng m và n là góc giữa hai đường thẳng a và b tương ứng vuông góc với m và n.

D. Góc giữa hai đường thẳng m và n là góc giữa hai đường thẳng a và b bất kỳ.

Câu 22. Trong không gian, cho hai đường thẳng a và b. Khẳng định nào sau đây là đúng?

A. Đường thẳng a và b vuông góc với nhau khi và chỉ khi chúng cắt nhau.

B. Đường thẳng a và b vuông góc với nhau khi và chỉ khi góc giữa chúng bằng 90°.

C. Đường thẳng a và b vuông góc với nhau khi và chỉ khi góc giữa chúng bằng 45°.

D. Đường thẳng a và b vuông góc với nhau khi và chỉ khi góc giữa chúng bằng 0°.

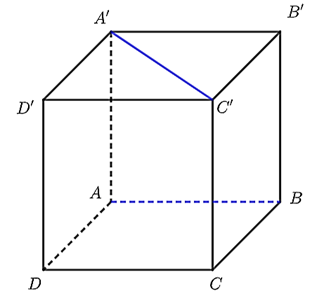
Câu 23. Cho hình lập phương ABCD.A'B'C'D' (như hình vẽ dưới).

Góc giữa hai đường thẳng AB và A'C' bằng

A. 60°.

B. 45°.

C. 90°.

D. 30°.

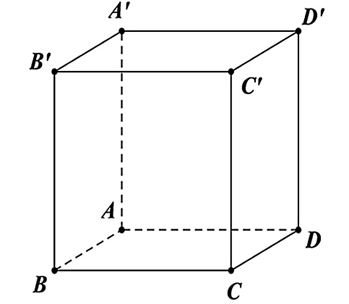
Câu 24. Cho hình lập phương ABCD.A'B'C'D' (như hình vẽ dưới).

Đường thẳng nào sau đây vuông góc với đường thẳng BC'?

A. A'D.

B. AC.

C. BB'.

D. AD'.

Câu 25. Trong không gian cho đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (α). Khẳng định nào sau đây đúng?

A. d // (α).

B. d ⊥ (α).

C. d ⊂ (α).

D. d cắt α.

Câu 26. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau (tham khảo hình vẽ).

Khẳng định nào sau đây là đúng?

A. AB ⊥ (BCD).

B. AC ⊥ (BCD).

C. AD ⊥ (BCD).

D. AD ⊥ (ABC).

Câu 27. Cho hai đường thẳng a, b và mp(P). Chỉ ra mệnh đề đúng trong các mệnh đề sau:

A. Nếu a // (P) và b ⊥ a thì b // (P).

B. Nếu a // (P) và b ⊥ (P) thì a ⊥ b.

C. Nếu a // (P) và b ⊥ a thì b ⊥ (P).

D. Nếu a ⊥ (P) và b ⊥ a thì b // (P).

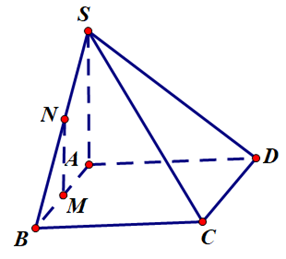
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD). Gọi M, N lần lượt là trung điểm của AB và SB (tham khảo hình vẽ).

Khẳng định nào sau đây là đúng?

A. AC ⊥ (SAD).

B. MN ⊥ (SBD).

C. BD ⊥ (SCD).

D. MN ⊥ (ABCD).

Câu 29. Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với mặt phẳng (ABCD). Gọi H là hình chiếu vuông góc của A lên mặt phẳng (SBC).

Khẳng định nào sau đây là khẳng định đúng?

A. H là chân đường vuông góc hạ từ A lên SB.

B. H là trọng tâm tam giác SBC.

C. H trùng với B.

D. H là trung điểm của SB.

Câu 30. Cho hai mặt phẳng (α), (β). Phát biểu nào sau đây đúng?

A. Nếu (α) cắt (β) thì (α) ⊥ (β).

B. Nếu ((α), (β)) = 0° thì (α) ⊥ (β).

C. Nếu ((α), (β)) = 45° thì (α) ⊥ (β).

D. Nếu ((α), (β)) = 90° thì (α) ⊥ (β).

Câu 31. Số cạnh bên của hình chóp cụt tứ giác đều là

A. 3.

B. 4.

C. 6.

D. 12.

Câu 32. Cho đường thẳng a vuông góc với mặt phẳng (α) và a ⊂ (β). Khẳng định nào sau đây là đúng?

A. (α) // (β).

B. (α) trùng (β).

C. $0°\le \left(\left(\alpha \right),\left(\beta \right)\right)<90°$.

D. (α) ⊥ (β).

Câu 33. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

B. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

D. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

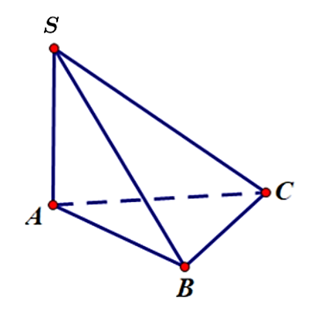
Câu 34. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, SA vuông góc với đáy (tham khảo hình vẽ).

Khẳng định nào sau đây sai?

A. (SAB) ⊥ (ABC).

B. (SAB) ⊥ (SAC).

C. (SAC) ⊥ (ABC).

D. (SAB) ⊥ (SBC).

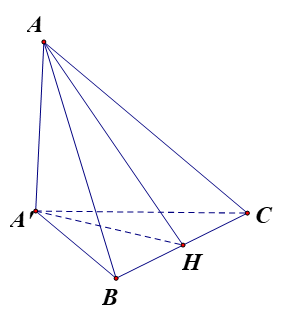
Câu 35. Cho tam giác ABC cân tại A có đường cao $AH=a\sqrt{3},BC=3a$, BC chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P) (như hình vẽ bên). Biết tam giác A'BC vuông tại A'. Gọi $\phi$ là góc giữa (P) và (ABC).

Chọn khẳng định đúng trong các khẳng định sau.

A. $\phi =60°$.

B. $\phi =45°$.

C. $\cos \phi =\frac{\sqrt{2}}{3}$.

D. $\phi =30°$.

II. Tự luận (3 điểm)

Bài 1. (1,0 điểm)

a) Tính giá trị của biểu thức $M={\left(3+2\sqrt{2}\right)}^{2019}\cdot {\left(3\sqrt{2}-4\right)}^{2018}$.

b) Tìm tất cả các giá trị thực của tham số m để hàm số $y=\log \left(x^2-2mx+4\right)$ có tập xác định là ℝ.

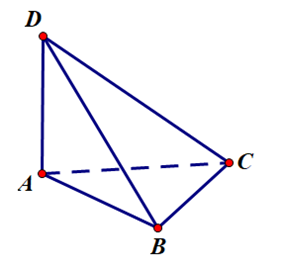
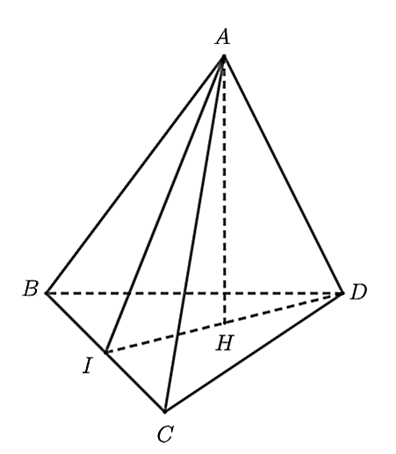
Bài 2. (1,0 điểm) Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm cạnh BC.

a) Chứng minh rằng BC ⊥ (AID).

b) Gọi AH là đường cao của tam giác AID. Chứng minh rằng AH ⊥ BD.

Bài 3. (1,0 điểm) Sự tăng trưởng của một loài vi khuẩn được tính theo công thức $f\left(t\right)=A{e}^{rt}$, trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng ( r > 0), t (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1 000 con và sau 10 giờ là 5 000 con. Hỏi sao bao lâu thì số lượng vi khuẩn tăng gấp 10 lần?

----------HẾT----------

ĐÁP ÁN ĐỀ SỐ 1

I. Bảng đáp án trắc nghiệm

1. D	2. B	3. D	4. C	5. C	6. A	7. A
8. D	9. C	10. D	11. D	12. B	13. C	14. D
15. D	16. A	17. C	18. C	19. C	20. A	21. A
22. B	23. B	24. A	25. B	26. D	27. B	28. D
29. A	30. D	31. B	32. D	33. B	34. B	35. D

II. Hướng dẫn giải tự luận

Bài 1. (1,0 điểm)

b) Điều kiện xác định của hàm số: $x^2-2mx+4>0$.

Hàm số có tập xác định là ℝ ⇔ $x^2-2mx+4>\mathrm{0,}\forall x\in ℝ$ ⇔ $m^2-4<0\iff -2<m<2$.

Bài 2. (1,0 điểm)

a) Vì tam giác ABC cân tại A có AI là trung tuyến nên AI đồng thời là đường cao, do đó AI ⊥ BC. (1)

Vì tam giác BCD cân tại D có DI là trung tuyến nên DI đồng thời là đường cao, do đó BI ⊥ BC. (2)

Từ (1) và (2) suy ra BC ⊥ (AID).

b) Vì AH là đường cao của tam giác AID nên AH ⊥ ID.

Từ đó suy ra AH ⊥ BD.

Bài 3. (1,0 điểm)

Số vi khuẩn ban đầu có 1 000 con và sau 10 giờ là 5 000 con. Áp dụng công thức $f\left(t\right)=A{e}^{rt}$, ta có: $f\left(10\right)=1000e^{r\cdot 10}$ = 5000. Suy ra $r=\frac{\ln 5}{10}$.

Giả sử t là thời gian để số lượng vi khuẩn tăng gấp 10 lần.

Khi đó ta có: $10000=1000e^{rt}$ ⇔ $e^{rt}=10\iff rt=\ln 10\iff t=\frac{\ln 10}{r}$

Do đó, $t=\ln 10:\frac{\ln 5}{10}=\frac{10\ln 10}{\ln 5}=10{\log }_{5}10\approx \mathrm{14,31}$.

Vậy sau khoảng 14,31 giờ thì số lượng vi khuẩn tăng gấp 10 lần.

----------HẾT----------

................................

................................

................................

Trên đây tóm tắt một số nội dung miễn phí trong bộ Đề thi Toán 11 năm 2024 mới nhất, để mua tài liệu trả phí đầy đủ, Thầy/Cô vui lòng xem thử:

Xem thử