Đề cương ôn tập Giữa kì 1 Toán 12 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm bộ đề cương ôn tập Giữa kì 1 Toán 12 Kết nối tri thức với bài tập trắc nghiệm, tự luận đa dạng có lời giải chi tiết giúp học sinh nắm vững được kiến thức cần ôn tập để đạt điểm cao trong bài thi Toán 12 Giữa kì 1.

Đề cương ôn tập Giữa kì 1 Toán 12 Kết nối tri thức

Xem thử

Chỉ từ 80k mua trọn bộ Đề cương ôn tập Giữa kì 1 Toán 12 Kết nối tri thức có lời giải bản word trình bày đẹp mắt, dễ dàng chỉnh sửa:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

Đề cương ôn tập Toán 12 Giữa kì 1 Kết nối tri thức gồm hai phần: Nội dung ôn tập và Bài tập ôn luyện, trong đó:

- 5 bài tập trắc nghiệm;

- 5 bài tập tự luận;

I. NỘI DUNG ÔN TẬP

Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Bài 1. Tính đơn điệu và cực trị của hàm số

- Tính đơn điệu của hàm số: Khái niệm, sử dụng bảng biến thiên xét tính đơn điệu của hàm số.

- Cực trị của hàm số: Khái niệm, cách tìm cực trị.

Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

- Định nghĩa giá trị lớn nhất, giá trị nhỏ nhất.

- Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn.

Bài 3. Đường tiệm cận của đồ thị hàm số

- Đường tiệm cận ngang.

- Đường tiệm cận đứng.

- Đường tiệm cận xiên.

Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số

- Sơ đồ khảo sát hàm số.

- Khảo sát và vẽ đồ thị hàm số đa thức bậc ba.

- Khảo sát và vẽ đồ thị hàm số phân thức hữu tỉ.

Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

- Tốc độ thay đổi của một đại lượng.

- Một vài bài toán tối ưu hóa đơn giản.

II. BÀI TẬP ÔN LUYỆN

A. TRẮC NGHIỆM

Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Bài 1. Tính đơn điệu và cực trị của hàm số

Câu 1. Tìm khoảng đồng biến của hàm số: .

A. $(0;+\infty )$.                                              

B. $(-\infty ;0)$ .                   

C. $(-\infty ;-\sqrt{2})$và $(0;\sqrt{2})$.                       

D. $(\sqrt{2};+\infty )$ .

Câu 2. Tìm khoảng nghịch biến của hàm số: $y=\frac{3-2x}{x+7}$.

A. $(-\infty ;7)$ .                                              

B. $(-\infty ;+\infty )$.                

C. $(-\infty ;-7)$ và $(-7;+\infty )$.                        

D. $(-10;+\infty )$ .

Câu 3. Hàm số $y=\sqrt{2x-x^2}$ nghịch biến trên khoảng nào.

A.  (0 ;1).  

B. $\left(-\infty ;1\right)$.

C. (1; 2).                      

D. $\left(1;+\infty \right)$.

Câu 4. Cho các hàm số sau:

$\left(I\right):y=-x^3+3x^2-3x+1;\left(II\right):y=\sin x-2x;$$\left(III\right):y=-\sqrt{x^3+2};\left(IV\right):y=\frac{x-2}{1-x}$.

Hỏi hàm số nào nghịch biến trên toàn trục số?

A. (I), (II).

B. (I), (II) và (III).                 

C. (I), (II) và (IV).       

D. (II), (III).

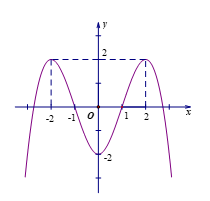
Câu 5. Cho hàm số y = f(x) xác định và liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Hỏi điểm cực tiểu của đồ thị hàm số y = f(x) là điểm nào?

A.  x = - 2

B. y = - 2 

C. M (0; - 2) 

D. N (2 ; 2)

Câu 6. Gọi M, n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số  $y=\frac{x^2+3x+3}{x+2}$. Khi đó giá trị của biểu thức $M^2-2n$ bằng:

A. 8.         

B. 7.          

C. 9.

D. 6.

Câu 7. Trong các câu sau câu nào đúng? Câu nào sai?

Cho hàm số $y=\frac{x+3}{x+2}$ .

A. Hàm số nghịch biến trên $ℝ\backslash \left\{-2\right\}$.

B. Hàm số nghịch biến trên $\left(-\infty ;-2\right)$  và $\left(-2;+\infty \right)$.

C. Hàm số đồng biến trên $ℝ$ .

D. Hàm số nghịch biến trên (- 4; - 3).

Câu 8. Cho hàm số $y=x^4-2x^2+1$ . Trong các mệnh đề sau mệnh đề nào đúng? Mệnh đề nào sai?

A. Hàm số có 3 điểm cực trị.

B. Hàm số đồng biến trên các khoảng $\left(-1;0\right)$ và $\left(1;+\infty \right)$.

C. Hàm số có 1 điểm cực trị.

D. Hàm số nghịch biến trên các khoảng $\left(-\infty ;-1\right)$ và (0; 1).

Câu 9. Cho hàm số $y=\sqrt{8+2x-x^2}$ . Xét tính đúng sai của các mệnh đề sau.

A. Tập xác định của hàm số là $D=\left[-2;4\right]$ .

B. Hàm số có $y^{\text{'}}=\frac{1-x}{\sqrt{8+2x-x^2}}$ .

C. Hàm số nghịch biến trên khoảng (1; 4).

D. Giá trị cực đại của hàm số là 0.

Câu 10. Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số $N\left(t\right)=-t^3+12t^2,0\le t\le 12$, trong đó N là số người bị nhiễm bệnh (đơn vị là trăm người) và t là thời gian (tuần). Gọi (a; b) là khoảng thời gian lâu nhất mà số người bị nhiễm bệnh tăng lên. Giá trị $P=2a^2-b^2=\mathrm{...............}$

Câu 11. Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức $N\left(t\right)=1000+\frac{100t}{100+t^2}$  (con), trong đó t là thời gian tính bằng giây. Hỏi thời gian bằng bao nhiêu để số lượng vi khuẩn đạt cực đại.

Điền đáp số: ………………

................................

................................

................................

B. TỰ LUẬN

Bài 1. Tìm các khoảng đơn điệu và các điểm cực trị của hàm số sau:

a) $y=-x^3+3x^2-4$ ;                               

b) $y=x^4+4x^3-1$.

Bài 2. Tìm các khoảng đơn điệu và cực trị của các hàm số sau

a) $y=\frac{2x+1}{x+1}$;                                          

b) $y=\frac{x^2+2x+2}{x+1}$ .

Bài 3. Tìm các khoảng đơn điệu và cực trị của các hàm số sau

a) $y=x^2+4\ln \left(3-x\right)$ ;                            

b) $y=\sqrt{x^2-2x}$ .

Bài 4. Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.

a) $f\left(x\right)=-x^3+3x^2+10$ trên đoạn $\left[-3;1\right]$ .

b) $f\left(x\right)=-2x^4+4x^2+3$  trên đoạn $\left[0;2\right]$ .

Bài 5. Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.

a) $f\left(x\right)=\frac{2x+3}{x+1}$  trên đoạn $\left[0;4\right]$ ;         

b) $f\left(x\right)=\frac{2x^2+4x+5}{x^2+1}$ trên R.

Bài 6. Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.

a) $y=e^{x^3-3x+3}$  trên đoạn $\left[0;2\right]$ ;               

b) $y=\frac{{\ln }^{2}x}{x}$  trên đoạn $\left[1;e^5\right]$.

Bài 7. Gọi A, B lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y=\frac{x+m^2+m}{x-1}$ trên đoạn $\left[2;3\right]$ . Tìm tất cả các giá trị thực của tham số m để $A+B=\frac{13}{2}$

................................

................................

................................

Xem thử