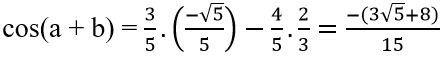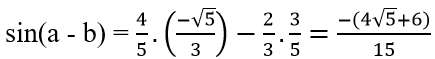Tính cos(a + π/3) , biết sina = 1/√3 và 0 < a < π/2

Bài 3: Công thức lượng giác

Bài 2 trang 154 Toán 10: Tính:

a) cos(a + π/3) , biết sina = 1/√3 và 0 < a < π/2

b) tan(a - π/4) , biết cosa = (-1)/3 và π/2 < a < π

c) cos(a + b), sin(a – b), biết sina = 4/5, 0 < a < 900 và sinb = 2/3, 900 < b < 1800.

Trả lời

cos(a + π/3) = cosa.cosπ/3 – sina.sinπ/3 (công thức cộng)

= 1/2cosa - √3/2.1/√3 = 1/2cosa - 1/2 (1)

Mà 0 < a < π/2 nên cos a > 0

Và sin2a + cos2a = 1 ⇒ cos2a = 1 - 1/3 = 2/3 ⇒ cosa = √6/3

Vậy (1)  cos(a + π/3) = 1/2cosa + 1/2= √6/6-1/2 = (√6-3)/6

b) 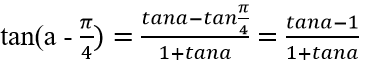(1)

Mà π/2 < a < π ⇒ tana < 0

Và cosa = -1/2 ⇒ tanα = -2√2

Từ (1), ta có: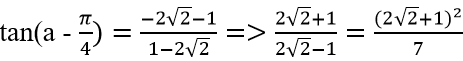

Vậy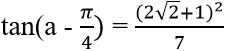

c) Vì 00 < a < 900 ⇒ cos a > 0

và sina = 4/5 ⇒ cosa = ± 3/5

⇒ cos a = 3/5

Vì 900 < a < 1800 ⇒ cosb < 0

và sinb = 2/3 ⇒ cosb = ± √5/3

⇒ cosb = (-√5)/3

Mà cos(a + b) = cosacosb – sinasinb; sin(a – b) = sinacosb – sinbcosa

Suy ra,