Trong một mặt phẳng Oxy cho điểm I(1; 1) và đường tròn tâm I bán kính 2

Bài 8: Phép đồng dạng

Bài 3 trang 33 Toán 11: Trong một mặt phẳng Oxy cho điểm I(1; 1) và đường tròn tâm I bán kính 2. Viết phương trình của đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được từ các thực hiện liên tiếp phép quay tâm O, góc 45º và phép vị tự tâm O, tỉ số √2.

Trả lời

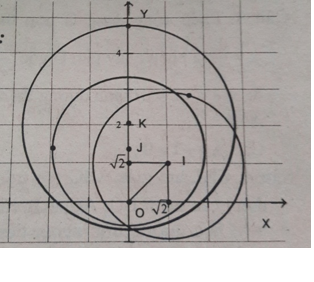
I(1; 1) nằm trên tia phân giác của góc phần tư thứ nhất nên OI hợp với tia Oy góc 45º.

Q_(O,45º) biến đường tròn tâm I(1; 1), bán kính R = 2 thành đường tròn tâm J(0; √2) và có cùng bán kính R’=2.

Q_(O,√2) biến đường tròn tâm J bán kính R’= 2 thành đường tròn tâm K bán kính R’’ thì 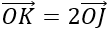nên K(0; 2) và R”=2√2.

Vậy ảnh của đường tròn tâm I qua phép đồng dạng là đường tròn tâm K có phương trình là x² + (y-2)² = 8.