Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ 4 đường thẳng Ax, By, Cz, Dt

Bài tập ôn tập chương 2 (phần Hình học)

Bài 4 trang 78 Toán 11 (Bài tập ôn tập chương 2): Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ 4 đường thẳng Ax, By, Cz, Dt ở cùng phía đói với mặt phẳng (ABCD), song song với nhau và không nằm trên mặt phẳng (ABCD). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A’, B’, C’, D’.

a) Chứng minh (Ax, By) // (Cz, Dt)

b) Gọi I = AC ∩ BD, J = A’C’ ∩ B’D’. chứng minh JJ’ // AA’

c) Cho AA’ = a, BB’ = b, CC’ = c. hãy tính DD’.

Trả lời

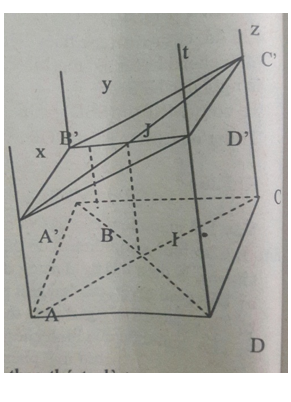
a) ABCD là hình bình hành ⇒ AB // CD    (1)

Theo giả thiết Ax // Dt     (2)

Từ (1) và (2) ⇒ (Ax, By) // (Cz, Dt)

b) Do (Ax, By) // (Cz, Dt) nên các giao tuyến A’D’ và B’C’ của các mặt phẳng này với (β) song song với nhau, suy ra A’B’ // D’C’

Tương tự ta cũng có: A’D’ // B’C’

Suy ra tứ giác A’B’C’D’ là hình bình hành. Vậy nên J là trung điểm của A’C’.

Mặt khắc: Ax // Cz nên tứ giác ACC’A’ là hình thang.

I, J lần lươt theo thứ tự là trung điểm các cạnh bên AC và A’C’ nên I là đường trung bình của hình thang này

Suy ra IJ // AA’

c) Vì IJ là đường trung bình của hình thang ACC’A’ nên

IJ = 1/2(AA’+ CC’)

Tương tự: IJ cũng là đường trung binh của hình thang BDD’B’ nên IJ = 1/2(BB’+ DD’)

Từ đây suy ra: AA’ + CC’ = BB’ + DD’⇒ DD’ = a +c – b