Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường

Ôn tập chương 3 phần hình học

Bài 61 trang 92 Toán 8 Tập 2: Tứ giác ABCD có AB = 4cm, BC = 20cm, CD = 25cm. DA = 8cm, đường chéo BD = 10cm.

a) Nếu cách vẽ tứ giác ABCD có kích thước đã cho ở trên.

b) Các tam giác ABD và BDC có đồng dạng với nhau không? Vì sao?

c) Chứng minh rằng AB // CD.

Trả lời

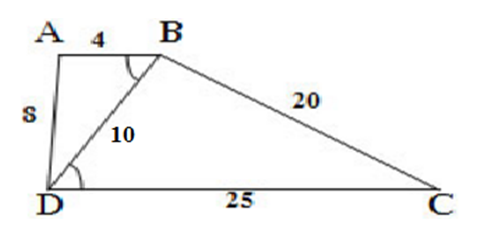
a) Giả sử tứ giác ABCD đã đựng được, ta thấy hai tam giác ABD và BDC đã được xác định vì đã biết có độ dài các cạnh

Cách dựng

Dựng đường thẳng a chia mặt phẳng ra hai nửa mặt phẳng (I) và (II). Trên a lấy đoạn BD = 10cm

Trên nửa mặt phẳng (I) dựng hai cung tròn ( B; 20cm) và (D; 25cm); ( do 20 + 25 > 10) nên hai cung này cắt nhau tại C. Nối C với B và C với D

Trên nửa mặt phẳng (II) dựng hai cung tròn ( B;4cm) và (D; 8cm) ( do 4 + 8 > 10) nên hai cung này cắt nhau tại A. Nối A với B với D thì ABCD là tứ giác cần dựng.

Chứng minh

Theo cách dựng ta có A ∈ (B, 4cm)

⇒ AB = 4cm, C ∈ (B, 20cm) ⇒ BC = 20cm

C ∈ (D,25cm) ⇒ CD = 25cm ; A ∈ (D,8cm) ⇒ DA = 8cm

Tam giác ABD và BDC nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng a

Vậy tứ giác ABCD thỏa mãn đề bài