Bài 19 trang 75 Toán 9 Tập 2

Luyện tập (trang 75-76)

Bài 19 trang 75 Toán 9 Tập 2: Cho đường tròn tâm O, đường kính AB, S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.

Bài giải:

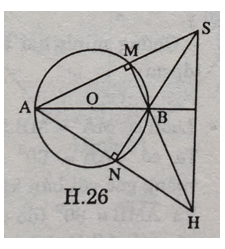
SH ⊥ AB

Ta có: ∠AMB = ∠ANB = 90° (góc nội tiếp chắn nửa đường tròn)

⇒ HM ⊥ SA và SN ⊥ HA.

⇒ B là trực tâm của ΔHAS.

⇒ AP là đường cao thứ ba của ΔHAS.

⇒ SH ⊥ AB.