Bài 54 trang 63 Toán 9 Tập 2

Ôn tập chương 4 (Câu hỏi - Bài tập)

Bài 54 trang 63 Toán 9 Tập 2: Vẽ đồ thị của hai hàm số y = x² và y = -x² trong cùng một hệ trục tọa độ.

a) Qua điểm B(0; 4) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số y = x² tại hai điểm M và M’. Tìm hoành độ của M và M’.

b) Tìm trên đồ thị của hàm số y = -x² điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:

- Ước lượng trên hình vẽ;

- Tính toán theo công thức.

Bài giải:

1) * Hàm số: y = x²

* Tập xác định: ∀x ∈R

* Bảng giá trị:

x	-4	-2	-1	0	1	2	4
y = x2	4	1		0		1	4

2) * Hàm số: y = -x²

* Tập xác định: ∀x ∈R

* Bảng giá trị:

x	-4	-2	-1	0	1	2	4
y = -x2	-4	-1	-	0	-	-1	-4

* Đồ thị của hai hàm số y = x² và y = -x²

a) Ta thấy đường thẳng (d) đi qua điểm B(0; 4) song song với Ox và cắt đồ thị hàm số y = x², nên hoành độ của M và M’ nghiệm đúng phương trình.

4 = x² ⇔ x² = 4² ⇔ x = ±4

Vậy hoành độ của M là x_M = 4 và hoành độ của M’ là x_M’ = -4

b₁) Điểm N trên đồ thị y = -x² có cùng hoành độ với M, thì x_N = x_M = 4 là nghiệm của phương trình.

y = -x²     (1)

Thay x_N = 4 vào (1)

Ta có: y_N = -.4² ⇔ y_N = -4

Vậy N(4; -4)

b₂) Điểm N’ trên đồ thị y = -x² có cùng hoành độ với M’, thì x_N’ = x_M’ = 4 là nghiệm của phương trình.

y = -x²     (1’)

Thay x_N’ = 4 vào (1’)

Ta có: y_N’ = -.4² ⇔ y_N’ = -4

Vậy N’(-4; -4)

b₂ * Phương trình đường thẳng NN’ có dạng y = ax + b     (2)

Tọa độ của N(4; -4) và N’(-4; -4) nghiệm đúng phương trình (2)

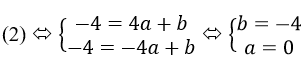
Vậy phương trình đường thẳng NN’ có dạng: y = -4

Do đó đường thẳng NN’ song song với Ox vì có a = 0

* Tìm tung độ N và N’ bằng hai cách.

- Cách 1: ước lượng trên hình vẽ.

Ta có: x_N = 4 và x_N’ = . Qua x_N và x_N’ vẽ hai đường thẳng song song với trục tung lần lượt cắt đồ thị hàm số y = -x² tại N và N’. Nối N và N’ cắt trục tung tại điểm có tung độ bằng -4. Khi đó -4 chính bằng tung độ của N và N’.

- Cách 2: Tính toán theo công thức: (làm tương tự câu b₁ và b₂).