Câu hỏi ôn tập chương 4 Đại số Toán 9 Tập 2

---

Ôn tập chương 4 (Câu hỏi - Bài tập)

Câu 1: Hãy vẽ đồ thị của các hàm số y = 2x²; y = -2x². Dựa ào đồ thị để trả lời các câu hỏi sau:

a) Nếu a > 0 thì hàm số y = 2x² đồng biến khi nào, nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?

Nếu a < 0 thì hàm số biến thiên như thế nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?

b) Đồ thị của hàm số y = 2x² có những đặc điểm gì (trường hợp a > 0; trường hợp a < 0)?

Bài giải:

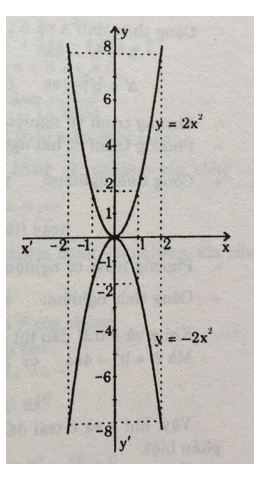
a) Đồ thị:

Nếu a > 0 thì đồ thị hàm số là parabol ở phía trên trục Ox, có hai nhánh:

- Nhánh bên phải biểu thị hàm số đồng biến khi x > 0.

- Nhánh bên trái biểu thị hàm số nghịch biến khi x < 0.

- Hàm số đạt giá trị nhỏ nhất bằng 0 khi x = 0

- Hàm số không đạt giá trị lớn nhất với bất cứ giá trị nào của x.

Nếu a < 0 thì đồ thị hàm số là parabol ở phía dưới trục Ox, có hai nhánh:

- Nhánh bên phải biểu thị hàm số nghịch biến khi x > 0.

- Nhánh bên trái biểu thị hàm số đồng biến khi x < 0.

- Hàm số đạt giá trị lớn nhất bằng 0 khi x = 0

- Hàm số không đạt giá trị nhỏ nhất với bất cứ giá trị nào của x.

b) Đặc điểm của đồ thị hàm số y = ax² ( a ≠ 0)

a > 0: Đồ thị đi qua điểm O, gốc của mặt phẳng tọa độ; nằm phía trên trục Ox; nhận trục Oy làm trục đối xứng, O là điểm thấp nhất của đồ thị.

a < 0 Đồ thị đi qua điểm o, gốc của mặt phẳng tọa độ; nằm phía dưới trục Ox; nhận trục Oy làm trục đối xứng, O là điểm cao nhất của đồ thị.

Câu 2: Đối với phương trình ax² + bx + c = 0 (a ≠ 0). Hãy viết công thức tính Δ,Δ'.

Khi nào thì phương trình vô nghiệm?

Khi nào phương trình có hai nghiệm phân biệt? Viết các công thức nghiệm

Khi nào phương trình có nghiệm kép? Viết các công thức nghiệm.

Vì sai khi a và c trái dấu thì phương trình có hai nghiệm phân biệt.

Bài giải:

Câu 3: Viết các hệ thức Vi-ét đối với nghiệm các phương trình bậc hai: ax² +bx + c = 0 (a ≠0)

Nêu điều kiện để phương trình ax² + bx + c = 0, a ≠ 0 có nghiệm bằng 1.

Viết công thức nghiệm thứ hai. Nhẩm nghiệm của phương trình:

1954x² + 21x – 1975 = 9

Nêu điều kiện để phương trình ax² bx + c = 0; a ≠ 0, có nghiệm bằng -1

Viết công thức nghiệm thứ hai. Nhẩm nghiệm của phương trình:

2005x² + 104x – 1901 = 0

Bài giải:

Câu 4: Nêu cách tìm hai số biết tổng S và tích P của chúng

Tìm hai số u và v trong mỗi trong trường hợp sau:

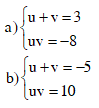
Bài giải:

Tương tự, S² – 4P = 25 – 40 < 0 nên không có u và v thỏa mãn đề bài.

Ta đưa phương trình ax⁴ + bx² + c = 0     (1) và dạng phương trình bậc hai theo t bằng cách đặt t = x² ( t ≥ 0): at² + bt + c = 0     (2)

- Nếu (2) có hai nghiệm phân biệt dương t₁; t₂ thì (1) có bốn nghiệm:

x₁ = ±√t₁ ; x₂ = ±√t₂

- Nếu (2) có một nghiệm dương t₁ và một nghiệm âm t₂ thì (1) có hai nghiệm: x₁ = √t₁; x₂ = -√t₁

- Nếu (2) có hai nghiệm đều âm thì (1) vô nghiệm

- Nếu (2) vô nghiệm (Δ < 0) thì (1) cũng vô nghiệm

Câu 5: Nêu cách giải phương trình trùng phương ax⁴ + bx² + c = 0 (a ≠ 0)

Bài giải:

- Đặt ẩn phụ t = x²     (1) (điều kiện t ≥ 0).

Khi đó phương trình đã cho tương đương với một phương trình bậc 2 ẩn t là:

at² + bt + c = 0     (2)

- Giải phương trình (2) để tìm t, so sánh với điều kiện.

- Thay giá trị t thỏa mãn vào (1) để tìm x.