Bài 61 trang 91 Toán 9 Tập 2

Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 61 trang 91 Toán 9 Tập 2:

a) Vẽ đường tròn tâm O, bán kính 2cm

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a)

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O, r)

Bài giải:

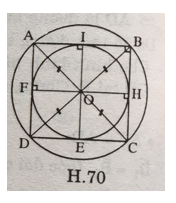
a) Vẽ đường tròn tâm O, bán kính 2cm

b) Vẽ hai đường kính AC và BD vuông góc với nhau trong (O). ABCD là hình vuông vẽ được

c) Tính độ dài r của (O; r). Kẻ OI vuông góc với AB tại I

ΔAOB vuông cân tại O.

⇒ AB = OA√2=2√2 (cm)

và OI cũng là trung tuyến ứng với cạnh huyền AB.

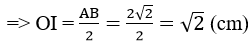
Đường tròn (O; OI) có OI vuông góc với AB tại I.

⇒ AB là tiếp tuyến của (O: OI)

Chứng minh tương tự ta có các cạnh BC, CD, DA là tiếp tuyến của (O; OI)

Do đó (O; I) là đường tròn nội tiếp hình vuông ABCD.

Vậy r = OI = √2 (cm)

* Vẽ đường tròn (O; r). Kẻ OI vuông góc với AB tại I vẽ đường tròn tâm O bán kính r = OI. Đó là đường tròn nội tiếp hình vuông ABCD.