Bài 62 trang 91 Toán 9 Tập 2

Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 62 trang 91 Toán 9 Tập 2:

a) Vẽ tam giác đều ABC cạnh a = 3cm

b) Vẽ tiếp đường tròn (O, R) ngoại tiếp tam giác đều ABC. Tính R

c) Vẽ tiếp đường tròn (O, r) nội tiếp tam giác đều ABC. Tính r.

d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O, R).

Bài giải:

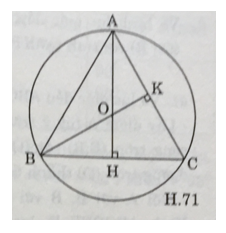
a) Vẽ tam giác đều ABC cạnh a = 3cm

- Vẽ đoạn BC = a = 3cm

- Vẽ hai cung tròn (B; 3cm) và (C; 3cm), chúng cắt nhau tại A. Ta có tam giác ABC là tam giác đều cạnh 3cm.

b) Vẽ tiếp đường tròn (O, R) ngoại tiếp tam giác đều ABC. Tính R

- Vẽ các đường cao AH và BK của ΔABC cắt nhau tại O. Ta có:

    O là trực tâm

    O là tâm đường tròn ngoại tiếp ΔABC, bán kính R = OA     (1)

    O là tâm đường tròn nội tiếp ΔABC, bán kính r = OH     (2)

    O là trọng tâm tam giác ABC.     (3)

    (Vì trong tam giác đều đường cao, trung tuyến, phân giác kẻ từ một đỉnh trùng nhau).

- Vẽ đường tròn tâm O bán kính OA. Đó là đường tròn (O; R) ngoại tiếp tam giác đều ABC.

* Tính R:

ΔAHB vuông tại H ta có:

Ghi chú:

* Trong bài tập 61, 62 ta chỉ nêu cách vẽ hình mà không chứng minh tại sao phải vẽ như vậy.

* Tính r ở câu c) bài 61 và tính R ở câu b) bài 62 có nhiều cách tính khác nhau. Các e học sinh có thể tìm cách tính khác với các tính trong các bài giải trên.

d) Vẽ tam giác đều IJK:

Tại ba đỉnh A, B, C vẽ các tiếp tuyến với (O; R) chúng cắt nhau tại I, J, K. ΔIJK là tam giác đều ngoại tiếp đường tròn (O).