Bài 64 trang 92 Toán 9 Tập 2

Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 64 trang 92 Toán 9 Tập 2: Trên một đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho sđ cung AB = 60°, sđ cung BC = 90° và sđ cung CD = 120°.

a) Tứ giác ABCD là hình gì?

b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác ABCD theo R.

Bài giải:

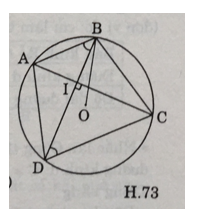
Gợi ý: Xem bài tập 63 để xác định được cung AB có số đo 60° trên (O). Khi có B, muốn xác định C ta vẽ ∠BOC = 90°, sau đó với hướng dẫn cách vẽ ở câu c) bài 63 ta xác định cung CD có số đo bằng 120°.

Do đó AC vuông góc với BD.

c) Gợi ý: Xem lại bài tập 61, 62, 63

Ta có: AB là cạnh của lục giác đều nội tiếp (O; R)

⇒ AB = R

* BC và AD căng cung số đo 90° là cạnh của hình vuông nội tiếp (O; R) ⇒ BC = AD = R√2

* CD căng cung có số đo 120° là cạnh của tam giác đều nội tiếp (O; R) ⇒ CD = R√3