Bài 63 trang 92 Toán 9 Tập 2
Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp
Bài 63 trang 92 Toán 9 Tập 2: Vẽ hình lục giác đều, hình vuông, tam giác đều nội tiếp đường tròn (O; R) rồi tính cạnh của hình lục giác đều đó theo R.
Bài giải:
a) Vẽ lục giác đều ABCDEF nội tiếp đường tròn (O; R)
- Lấy điểm A tùy ý trên (O), vẽ cung tròn (A; R) cắt (O) tại B, vẽ tiếp cung tròn (B; R) cắt (O) tại C, tiếp tục làm như vậy ta sẽ chia được đường tròn (O) thành 6 cung bằng nhau.
- Nối A với B, B với C… F với A.
Hình ABCDEF là lục giác đều nội tiếp đường tròn (O).
* Tính cạnh của lục giác đều:
ABCDEF là lục giác đều
⇒ AB = BC = CD = DE = EF = FA
⇒ sđ cung AB = 60° ⇒ ∠AOB = 60°
⇒ Tam giác AOB đều.
Vậy cạnh của lục giác đều bằng R.
b) Vẽ hình vuông nội tiếp (O; R) và tính cạnh hình vuông (xem bài tập 61)
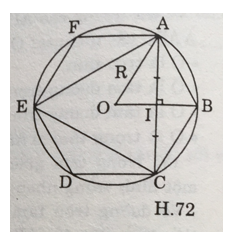
c) Vẽ tam giác vuông nội tiếp (O; R)
Ta vẽ như đã vẽ lục giác đều (câu a). Sauk hi chia (O) thành 6 phần bằng nhau, thay vì nối A với B thì ta nối A với C; C với E; E với A, ta sẽ được tam giác ACE là tam giác đều nội tiếp (O; R)
Tính cạnh của tam giác đều ACE theo R:
Ta có: sđ cung AB = sđ cung BC ⇒ IA = IC (I là giao điểm của BC với OB) (1)
⇒ OI vuông góc với AC
Tam giác OAI vuông tại I và ∠AOB = 60° (cmt)
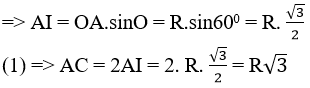
Vậy cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng R√3
* Ghi nhớ: Từ bài tập 61, 62, 63/ bài 8 SGK ta có công thức tính cạnh của một số đa giác đều nội tiếp như sau:
| ĐA GIÁC ĐỀU NỘI TIẾP ĐƯỜNG TRÒN (O; R) | ĐỘ DÀI CẠNH CỦA ĐA GIÁC ĐỀU THEO R | CĂNG CUNG CÓ SỐ ĐO |
|---|---|---|
| Lục giác đều cạnh a | a = R | 60° |
| Hình vuông cạnh a | a = R√2 | 90° |
| Tam giác đều cạnh a | a = R√3 | 120° |

