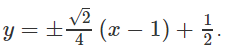Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 1)^2 + (y - 2)^2 = 4 và hai điểm A(1 ; 4), B(1; 1/2)

Ôn tập cuối năm

Bài 13 trang 202 Sách bài tập Hình học 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 1)² + (y - 2)² = 4 và hai điểm A(1 ; 4), B(1; 1/2). Viết phương trình đường thẳng d đi qua B cắt đường tròn (C) tại M, N sao cho AMN có diện tích lớn nhất.

Lời giải:

    (Xem hình 3.36)

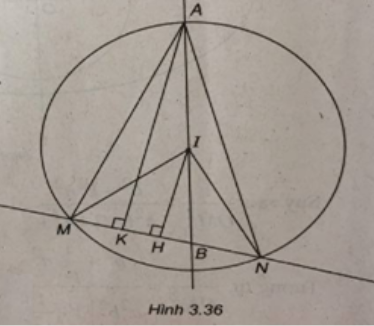
    Đường tròn (C) có tâm I(1;2) và có bán kính R = 2.

    Ta có: x_A = x_I = x^B

    Suy ra A, I, B cùng thuộc đường thẳng có phương trình x = 1.

    Ta có:

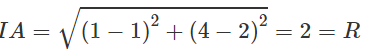
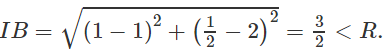
    Suy ra điểm A nằm trên đường tròn và điểm B nằm trong hình tròn.

    Gọi H và K là hình chiếu của I và A xuống đường thẳng d.

    Ta có:

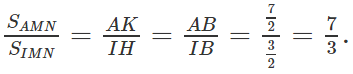
    Suy ra S_AMN = 7S_IMN/3

    = (7/3). (1/2). IM. IN. sin MIN = (14/3).sin MIN ≤ 14/3

    S_AMNlớn nhất ⇔ sin MIN = 1 ⇔ góc MIN = 90^ο

    ⇔ IH = (R√2)/2 ⇔ d(I,MN) = √2

    Phương trình đường thẳng MN là :

    y - 0,5 = k(x - 1) ⇔ 2kx - 2y + (1 - 2k) = 0

    Ta có: d(I,MN) = √2

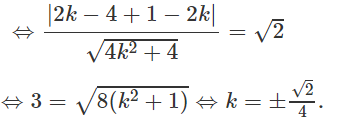
    Vậy phương trình đường thẳng d là: