Trong mặt phẳng tọa độ Oxy, cho elip (E) và điểm A(-1; 0,5). Gọi d là đưởng thẳng đi qua A có hệ số góc là m

Ôn tập cuối năm

Bài 18 trang 203 Sách bài tập Hình học 10: Trong mặt phẳng tọa độ Oxy, cho elip (E): và điểm A(-1; 0,5). Gọi d là đưởng thẳng đi qua A có hệ số góc là m. Xác định m để d cắt (E) tại hai điểm phân biệt M và N sao cho A là trung điểm của MN.

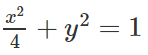
Lời giải:

    Phương trình đường thẳng d có dạng: y - 0,5 = m(x + 1) ⇔ y = m(x + 1) + 0,5.

    Phương trình hoành độ giao điểm của d và (E) là:

    x²/4 + (mx + m + 0,5)² = 1

    ⇔ x² + 4[mx + (m + 0,5)]² = 4

    ⇔ (4m² + 1)x² + 4[(2m + 1)m]x + 4(m + 0,5)² - 4 = 0

    A là trung điểm của MN

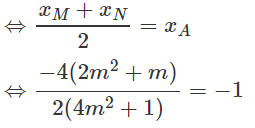
    ⇔ 4m² + 2m = 4m² + 1 ⇔ m = 0,5