Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật biết tọa độ hai đỉnh đối diện là (1;-5) và (6;2)

Ôn tập cuối năm

Bài 14 trang 203 Sách bài tập Hình học 10: Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật biết tọa độ hai đỉnh đối diện là (1;-5) và (6;2), phương trình của một đường chéo là 5x + 7y - 7 = 0. Tìm tọa độ các đỉnh còn lại của hình chữ nhật.

Lời giải:

    (Xem hình 3.37)

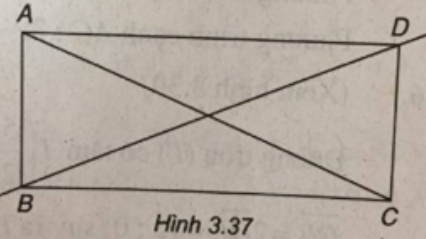
    Đặt A(1 ; -5), C(6 ; 2) và BD có phương trình: 5x + 7y - 7 = 0.

    Đặt x_B = 7t ta có y_B = 1 - 5t.

    Vậy B(7t; 1 - 5t).

    Suy ra: vectơ BA = (1 - 7t; -6 + 5t) và vectơ BC = (6 - 7t; 1 + 5t).

    Ta có:

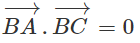
    ⇔ (1 - 7t)(6 - 7t) + (1 + 5t)(-6 + 5t) = 0

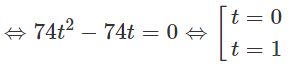
    Vậy B(0;1); D(7;-4) hoặc B(7;-4); D(0;1).