Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có đỉnh A(2;-1), phương trình một đường chéo

Ôn tập cuối năm

Bài 19 trang 203 Sách bài tập Hình học 10: Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có đỉnh A(2;-1), phương trình một đường chéo là x - 7y + 15 = 0 và độ dài cạnh AB = 3√2. Tìm tọa độ các đỉnh A, C, D biết y_B là một số nguyên.

Lời giải:

    Do tọa độ A không thỏa mãn phương trình đường thẳng x - 7y + 15 = 0 nên phương trình đường chéo BD là : x - 7y + 15 = 0, tọa độ điểm B là B(7t - 15; t).

    Ta có :

    AB = 3√2 ⇔ (7t - 17)² + (t + 1)² = 18

    ⇔ 50t² - 236t + 272 = 0

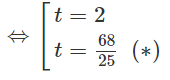
    ( (∗) loại)

    Vậy B(-1 ; 2)

    Ta có: = (-3;3) = -3(1;-1)

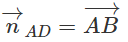
    Phương trình đường thẳng AD là :

    1(x - 2) - 1(y + 1) = 0

    ⇔ x - y - 3 = 0

    Tọa độ điểm D là nghiệm của hệ:

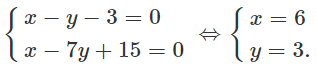
    Vậy D(6 ; 3).

    Ta có AC và BD cắt nhau tại trung điểm I.

    Suy ra:

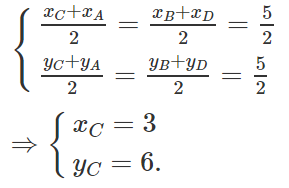
    Vậy C(3 ; 6).