Bài tập trắc nghiệm trang 204, 205, 206, 207, 208, 209 Sách bài tập Hình học 10

---

Ôn tập cuối năm

Bài tập trắc nghiệm trang 204, 205, 206, 207, 208, 209 Sách bài tập Hình học 10:

    Bài 1: Cho hình bình hành ABCD. Tổng vectơ là:

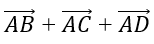
Lời giải:

Áp dụng quy tắc hình bình hành ta có:

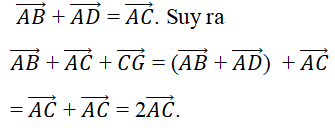
Đáp án: A

    Bài 2: Cho tam giác ABC có trọng tâm là G. Đặt . Vectơ AG bằng:

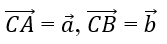
Lời giải:

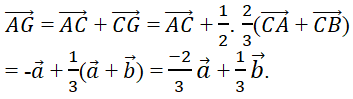
Đáp án: B

    Bài 3: Cho E, F lần lượt là trung điểm của cạnh AB và AC của tam giác ABC không cân tại A. Tập hợp các điểm M thỏa mãn là:

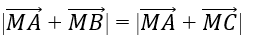
    A. Đường trung trực của EF          B. Đường thẳng BA

    C. Đường trung trực của BC          D. Đường thẳng BC

Lời giải:

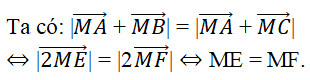
Vậy tập hợp các điểm M là đường trung trực của EF.

Đáp án: A

    Bài 4: Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho BI = 2IC. Khẳng định nào sau đây là đúng?

Lời giải:

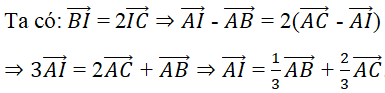
Đáp án: A

    Bài 5: Cho tam giác ABC đều cạnh a. Gọi G là trọng tâm tam giác ABC. Trong các đẳng thức sau đẳng thức nào sai?

Lời giải:

Gọi M là trung điểm BC, ta có: |GB→ + GC→| = 2|GM→| = 1/3a√3. Mệnh đề C sai.

Đáp án: C

    Bài 6: Trong mặt phẳng Oxy, cho hai điểm A(0;3), B(3;1). Tọa độ điểm M thỏa mãn là:

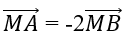
    A. (6;-7)          B. (-6;7)

    C. (-6;-1)          D. (6;-1)

Lời giải:

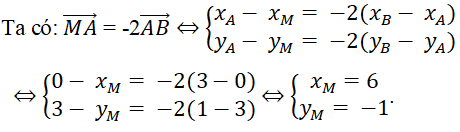
Đáp án: D

    Bài 7: Trong mặt phẳng Oxy, cho hình bình hành ABCD có A(-2;0), B(3;-2) và G(-1;2) là trọng tâm tam giác ADC. Tọa độ đỉnh D là:

    A. (-2;4)          B. (3;4)

    C. (3;-4)          D. (-3;4)

Lời giải:

G là trọng tâm tam giác ADC ⇔ DG→ = 1/3 DB→

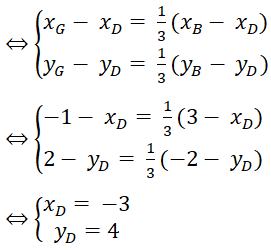
Đáp án: D

    Bài 8: Cho . Tìm tọa độ

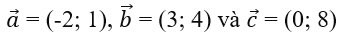
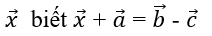
Lời giải:

x→ = b→ - c→ - a→ = (5; -5).

Đáp án: C

    Bài 9: Trong mặt phẳng Oxy, cho tam giác MNP có M(1;1), N(5;3) và P thuộc trục Oy, trọng tâm G của tam giác nằm trên trục Ox. Tọa độ của điểm P là:

    A. (2;0)          B. (0;-2)

    C. (2;-4)          D. (0;-4)

Lời giải:

P thuộc trục Oy nên x_P = 0. Trọng tâm G của tam giác nằm trên trục Ox nên y_G = 0, suy ra y_P = -4.

Đáp án: D

    Bài 10: Trong các khẳng định sau, tìm khẳng định sai:

    A. sin 90^ο > sin 180^ο          B. sin 90^ο13' > sin 90^ο14'

    C. sin 45^ο > sin 46^ο          D. sin 110^ο > sin 112^ο

Lời giải:

0^o < 45^o < 46^o < 90^o nên sin45^o < sin46^o.

Đáp án: C

    Bài 11: Giá trị của biểu thức mcos 90^ο + psin 180^ο bằng:

    A. m          B. n

    C. p          D. m + n

Lời giải:

cos90^o = 0, sin180^o = 0, sin90^o = 1.

Đáp án: B

    Bài 12: Để tính cos 120^ο, một học sinh thực hiện các bước như sau:

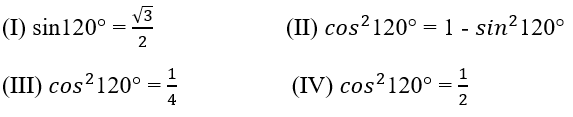
    Lập luận trên không đúng từ bước nào?

    A. (I)          B. (II)          C. (III)          D. (IV)

Lời giải:

Vì 90^o < 120^o < 180^o nên cos120^o < 0.

Đáp án: D

    Bài 13: Giá trị của biểu thức S = sin²3^ο + sin²15^ο + sin²75^ο + sin²87^ο bằng:

    A. S = 1          B. S = 0

    C. S = 2          D. S = 4

Lời giải:

sin87^o = cos3^o, sin75^o = cos15^o nên S = 2.

Đáp án: C

    Bài 14: Rút gọn biểu thức S = cos(90^ο - x)sin(180^ο - x) - sin(90^ο - x)cos(180^ο - x) ta được:

    A. S = 1          B. S = 0

    C. S = sin²x - cos²x          D. S = 2sinxcosx

Lời giải:

Áp dụng công thức sina.cosb – sinb.cosa = sin(a – b) ta có S = 1.

Đáp án: A

    Bài 15: Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Tích vô hướng bằng:

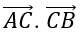
    A. 3a²          B. a²          C. -a²          D. -3a²

Lời giải:

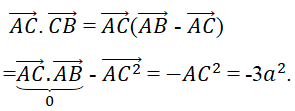
Đáp án: D

    Bài 16: Trong mặt phẳng Oxy cho các điểm A(1;1), B(2;4), C(10;-2). Góc BAC bằng bao nhiêu?

    A. 90^ο          B. 60^ο          C. 45^ο          D. 30^ο

Lời giải:

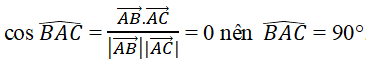
Đáp án: D

    Bài 17: Trong mặt phẳng Oxy cho các điểm A(1;1), B(2;4), C(10;-2). Tích vô hướng bằng:

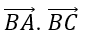
    A. 30          B. 10          C. -10          D. -30

Lời giải:

BA→ = (-1; -3), BC→ = (8; -6) nên BA→. BC→ = -8 + 18 = 10.

Đáp án: B

    Bài 18: Tam giác ABC có các cạnh a, b, c. cosB bằng biểu thức nào sau đây?

Lời giải:

Áp dụng định lý côsin ta chọn D.

Đáp án: D

    Bài 19: Độ dài trung tuyến m_c ứng với cạnh c của tam giác ABC bằng biểu thức nào sau đây?

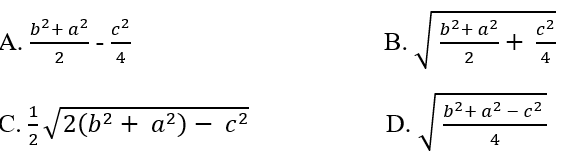
Lời giải:

Áp dụng công thức b² + a² = 2m_c² + c²/2.

Đáp án: C

    Bài 20: Gọi S là diện tích ta, giác ABC. Trong các khẳng định sau, tìm khẳng định đúng.

    A. S = a.h_a          B. S = abcosC/2

    C. S = abc/4R          D. S = absinC

Lời giải:

Đáp án: C

    Bài 21: Tam giác ABC có ba cạnh thỏa mãn hệ thức: a² = b² - c² - ac. Góc B bằng bao nhiêu?

    A. 150^ο          B. 120^ο

    C. 60^ο          D. 30^ο

Lời giải:

Ta có cosB = (-1)/2.

Đáp án: B

    Bài 22: Tam giác ABC có các cạnh là a = 6, b = 4√2, c = 2. M là điểm trên cạnh BC sao cho BM = 3. Độ dài đoạn AM bằng bao nhiêu?

    A. 3          B. 9          C. 4          D. (√108)/2

Lời giải:

Ta có M là trung điểm BC. Áp dụng công thức b² + c² = 2m_a² + a²/2.

Đáp án: A

    Bài 23: Cho tam giác ABC có ba cạnh thỏa mãn hệ thức: b + c = 2a. Trong các mệnh đề sau, mện đề nào đúng?

    A. cosB + cosC = 2cosA          B. sinB + sinC = 2sinA

    C. sinB + sinC = (sinA)/2          D. sinB + cosC = 2sinA

Lời giải:

Thay b = 2R.sinB, c = 2R.sinC, a = 2R.sinA.

Đáp án: B

    Bài 24: Gọi S = m²_a + m²_b + m²_c là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các khẳng định sau, khẳng định nào đúng?

    A. S = 3(a² + b² + c²)/4          B. S = (a² + b² + c²)

    C. S = 3(a² + b² + c²)/2          D. S = 3(a² + b² + c²)

Lời giải:

Thay m_a² = 1/2(b² + c² - a²/2), 〖m_b〗² = 1/2(a² + c² - b²/2), 〖m_c〗² = 1/2(a² + b² - c²/2).

Đáp án: A

    Bài 25: Cho tam giác ABC, biết cạnh a = 17,4; góc B = 44^ο33'; góc C = 64ο. Cạnh b bằng bao nhiêu?

    A. 16,5          B. 12,9

    C. 15,6          D. 22,1

Lời giải:

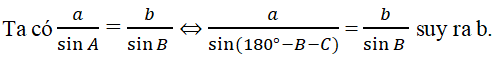
Đáp án: B

    Bài 26: Cho tam giác ABC biết các cạnh a = 16,8; góc B = 56^ο13'; góc C = 71^ο. Cạnh c bằng bao nhiêu?

    A. 29,9          B. 14,1

    C. 17,5          D. 19,9

Lời giải:

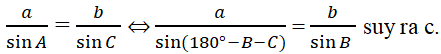
Đáp án: D

    Bài 27: Cho tam giác ABC biết các cạnh a = 49,4; b = 26,4; góc C = 47^ο20'. Cạnh c bằng bao nhiêu?

    A. 64          B. 37

    C. 28,5          D. 136,9

Lời giải:

Áp dụng công thức c² = a² + b² – 2ac.cosC.

Đáp án: B

    Bài 28: Cho tam giác ABC biết các cạnh a = 24; b = 13; c = 15. Góc A bằng:

    A. 33^ο34'          B. 117^ο49'

    C. 28^ο37'          D. 58^ο24'

Lời giải:

Áp dụng công thức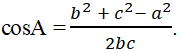

Đáp án: B

    Bài 29: Cho tam giác ABC biết các cạnh a = 13; b = 14; c = 15. Góc B bằng:

    A. 59^ο49'          B. 53^ο7'

    C. 59^ο29'          D. 62^ο22'

Lời giải:

Áp dụng công thức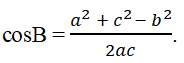

Đáp án: C

    Bài 30: Cho tam giác ABC có tọa độ các đỉnh là A(1;2), B(3;1), C(5;4). Phương trình đường cao vẽ từ A là:

    A. 2x + 3y - 8 = 0          B. 3x - 2y - 5 = 0

    C. 5x - 6y + 7 = 0          D. 3x - 2y + 5 = 0

Lời giải:

Đường cao vẽ từ A có vectơ pháp tuyến BC→ = (2;3) nên có phương trình là: 2(x – 1) + 3(y – 2) = 0 hay 2x + 3y – 8 = 0.

Đáp án: A

    Bài 31: Cho tam giác ABC với A(-1;1), B(4;7), C(3;-2). Phương trình tham số của trung tuyến CM là:

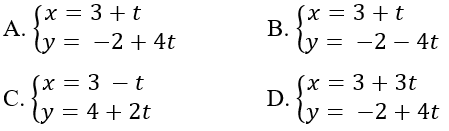
Lời giải:

Ta có trung điểm của AB là điểm M(3/2; 4). Trung tuyến CM đi qua điểm C(3;-2) và có vectơ chỉ phương (CM→ = ((-3)/2;6) = (-3)/2(1; -4) nên có phương trình tham số: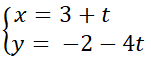

Đáp án: B

    Bài 32: Cho phương trình tham số của đường thẳng d: . Phương trình tổng quát của đường thằng d là:

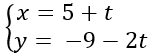
    A. 2x + y - 1 = 0          B. 2x + y + 1 = 0

    C. x + 2y + 2 = 0          D. x + 2y - 2 = 0

Lời giải:

2x + y – 1 = 0.

Đáp án: A

    Bài 33: Phương trình nào sau đây là phương trình đường tròn?

    A. x² + 2y² - 4x - 8y + 1 = 0          B. 4x² + y² - 10x - 6y - 2 = 0

    C. x² + y² - 2x - 8y + 20 = 0          D. x² + y² - 4x + 6y - 12 = 0

Lời giải:

x² + y² – 4x + 6y – 12 = 0.

Đáp án: D

    Bài 34: Cho đường tròn (C): x² + y² + 2x + 4y - 20 = 0. Trong các khẳng định sau, tìm khẳng định sai.

    A. (C) có tâm I(1;2)

    B. (C) có bán kính R = 5

    C. (C) đi qua điểm M(2;2)

    D. (C) không đi qua điểm A(1;1)

Lời giải:

(C) có tâm I(-1; -2). Mệnh đề A sai.

Đáp án: A

    Bài 35: Cho đường tròn (C): x² + y² - 4x - 2y = 0 và đường thẳng Δ: x + 2y + 1 = 0.

    Trong các khẳng định sau, tìm khẳng định đúng.

    A. Δ đi qua tâm của (C).

    B. Δ cắt (C) tại hai điểm.

    C. Δ tiếp xúc (C).

    D. Δ không có điểm chung với (C)

Lời giải:

Đường tròn (C) có tâm I(2;1) và có bán kính R = √5. Ta có:

Suy ra Δ tiếp xúc với (C).

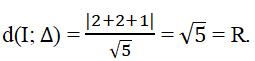
Đáp án: C

    Bài 36: Cho ba điểm A(3;5), B(2;3), C(6;2). Đường tròn ngoại tiếp tam giác ABC có phương trình là:

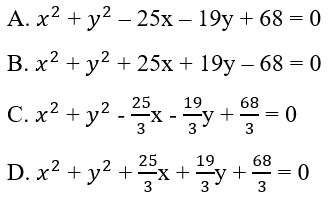
Lời giải:

Phương trình đường tròn ngoại tiếp tam giác ABC có dạng:

x² + y² – 2ax – 2by + c = 0. Thay tọa độ của ba điểm A, B, C vào ta được hệ phương trình:

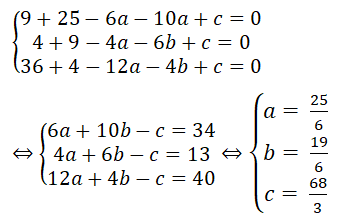
Suy ra phương trình đường tròn ngoại tiếp tam giác ABC là

x² + y² - 25/6 x - 19/6 y + 68/3 = 0. Chọn C.

Đáp án:

    Bài 37: Lập phương trình chính tắc của elip có hai đỉnh (-3;0), (3;0) và hai tiêu điểm (-1;0), (1;0) ta được:

Lời giải:

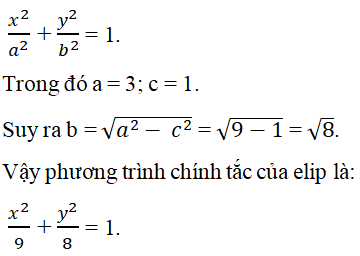
Đáp án: C

    Bài 38: Cho elip (E): 4x² + 9y² = 36. Trong các khẳng định sau, tìm khẳng định sai.

    A. (E) có trục lớn bằng 6.          B. (E) có trục nhỏ bằng 4

    C. (E) có tiêu cự bằng √5          D. (E) có tâm sai bằng (√5)/3

Lời giải:

(E) có tiêu cự bằng 2c = 2√5. Vậy mệnh đề C sai.

Đáp án: C

    Bài 39: Cho elip (E): và đường thẳng Δ: x + y + 5 = 0. Tích các khoảng cách từ hai tiêu điểm của (E) đến Δ bằng:

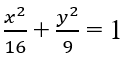
    A. 16          B. 9

    C. 81          D. 7

Lời giải:

(E) có hai tiêu điểm F₁(-√7;0), F₂(√7;0)

d(F₁,Δ). d(F₂,Δ) = 9.

Đáp án: B