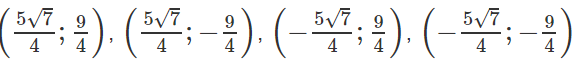Cho elip (E): 9x^2 + 25y^2 = 225. Tìm tọa độ hai điểm F1, F2 và các đỉnh của (E)

Bài 3: Phương trình đường elip

Bài 3.34 trang 164 Sách bài tập Hình học 10: Cho elip (E): 9x² + 25y² = 225

    a) Tìm tọa độ hai điểm F₁, F₂ và các đỉnh của (E).

    b) Tìm M ∈ (E) sao cho M nhìn F₁, F₂ dưới một góc vuông.

Lời giải:

    (E): 9x² + 25y² = 225 ⇔

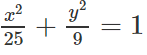
    a) Ta có: a² = 25, b² = 9

    ⇒ a = 5, b = 3

    Ta có: c² = a² - b² = 16

    ⇒ c = 4

    Vậy (E) có hai tiêu điểm là : F₁(-4; 0) và F₂(4; 0) và có bốn đỉnh là A₁(-5; 0), A₂(5; 0), B₁(0; -3), B₂(0; 3)

    b) Gọi M(x; y) là điểm cần tìm, ta có :

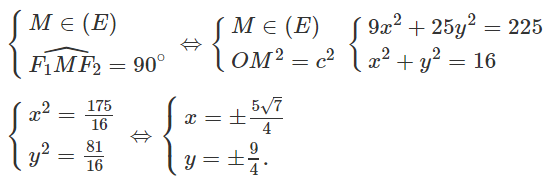
    Vậy có bốn điểm M thỏa mãn điều kiện của đề bài là :