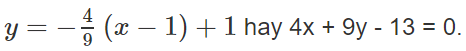Cho elip (E): 4x^2 + 9y^2 = 36 và điểm M(1; 1). Viết phương trình đường thẳng d đi qua M và cắt (E)

Bài 3: Phương trình đường elip

Bài 3.36 trang 164 Sách bài tập Hình học 10:Cho elip (E): 4x² + 9y² = 36 và điểm M(1; 1). Viết phương trình đường thẳng d đi qua M và cắt (E) tại hai điểm A và B sao cho M là trung điểm của AB.

Lời giải:

    (E): 4x² + 9y² = 36

    Xét đường thẳng d đi qua điểm M(1;1) và có hệ số góc k. Ta có phương trình của

    d: y - 1 = k(x - 1) hay y = k(x - 1) + 1 (2)

    Thay (2) vào (1) ta được

    4x + 9[k(x - 1) + 1]² = 36

    ⇔ (9k² + 4)x² + 18k(1 - k) + 9(1 - k)² - 36 = 0

    Ta có : d cắt (E) tại hai điểm A, B thỏa mãn

    MA = MB khi và chỉ khi phương trình (3) có hai nghiệm x_A, x_B sao cho:

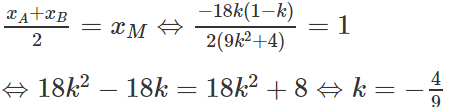
    Vậy phương trình của d là :