Cho đường tròn (C): x^2 + y^2 - 2x - 6y + 6 = 0 và điểm M(2;4). Chứng minh rằng điểm M nằm trong (C)

Ôn tập chương 3

Bài 3.50 trang 166 Sách bài tập Hình học 10: Cho đường tròn (C): x² + y² - 2x - 6y + 6 = 0 và điểm M(2;4).

    a) Chứng minh rằng điểm M nằm trong (C) ;

    b) Viết phương trình đường thẳng d đi qua M và cắt đường tròn (C) tại hai điểm A, B sao cho M là trung điểm của đoạn AB.

Lời giải:

    a) (C): x² + y² - 2x - 6y + 6 = 0

    ⇒ (C) có: (R là bán kính)

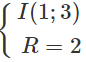
    IM = √2 < R ⇒ M nằm trong (C)

    b) Đường thẳng d cắt đường tròn (C) tại hai điểm A, B sao cho M là trung điểm của đoạn thẳng AB ⇒ d ⊥ IM tại M

    Phương trình đường thẳng:

    d: - qua M(2;4)

     - nhận vectơ IM = (1; 1)làm vectơ pháp tuyến

    ⇒ d: 1.(x - 2) + 1.(y - 4) = 0

    ⇒ d: x + y - 6 = 0