Trong mặt phẳng Oxy cho đường tròn (T) có phương trình: x^ + y^2 - 4x - 2y + 3 = 0. Tìm tọa độ tâm

Ôn tập cuối năm

Bài 5 trang 201 Sách bài tập Hình học 10: Trong mặt phẳng Oxy cho đường tròn (T) có phương trình:

    x² + y² - 4x - 2y + 3 = 0

    a) Tìm tọa độ tâm và tính bán kính của đường tròn (T).

    b) Tìm m để đường thẳng y = x + m có điểm chung với đường tròn (T).

    c) Viết phương trình tiếp tuyến Δ với đường tròn (T) biết rằng Δ vuông góc vơi đường thẳng d có phương trình x - y + 2006 = 0.

Lời giải:

    a) Đường tròn (T) có tâm là điểm (2 ; 1) và có bán kính bằng √2

    b) Đường thẳng l: x - y + m = 0. Ta có:

    l có điểm chung với (T)

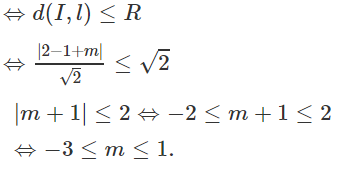
    c) Δ ⊥ d nên Δ có phương trình x + y + c = 0.

    Ta có : Δ tiếp xúc với (T) khi và chỉ khi:

    d(I; Δ) = R

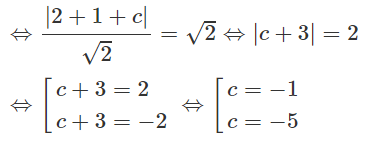
    Vậy có hai tiếp tuyến với (T) thỏa mãn đề bài là :

     Δ₁: x + y - 1 = 0

     Δ₂: x + y - 5 = 0