Trong mặt phẳng Oxy cho elip (E) có tiêu điểm thứ nhất là (-√3;0) và đi qua điểm

Ôn tập cuối năm

Bài 6 trang 201 Sách bài tập Hình học 10: Trong mặt phẳng Oxy cho elip (E) có tiêu điểm thứ nhất là (-√3;0) và đi qua điểm

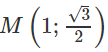
    a) Hãy xác định tọa độ các đỉnh của (E).

    b) Viết phương trình chính tắc của (E).

    c) Đường thẳng đi qua tiêu điểm thứ hai của elip (E) và vuông góc với trục Ox và cắt (E) tại hai điểm C và D. Tính độ dài đoạn thẳng CD.

Lời giải:

    a) (E) có tiêu điểm F₁(-√3;0) nên c = √3.

    Phương trình chính tắc của (E) có dạng

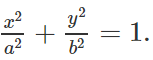
    Ta có: ∈ (E)

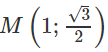
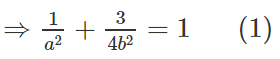
    Và a² = b² + c² = b² + 3

    Thay vào (1) ta được :

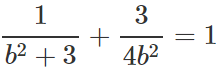
    ⇔ 4b² + 3b² + 9 = 4b²(b + 3)

    ⇔ 4b⁴ + 5b² - 9 = 0 ⇔ b² = 1

    Suy ra: a² = 4

    Ta có a = 2 ; b = 1.

    Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0), (0 ; -1) và (0 ; 1).

    b) Phương trình chính tắc của (E) là :

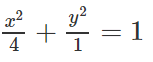
    c) (E) có tiêu điểm thứ hai là điểm (√3;0). Đường thẳng Δ đi qua điểm (√3;0) và vuông góc với Ox có phương trình x = √3

    Phương trình tung độ giao điểm của Δ và (E) là :

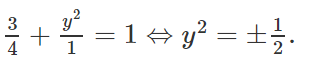
    Suy ra tọa độ của C và D là :

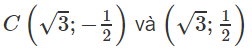
    Vậy CD = 1.