Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0;2), B(-2;-2) và C(4;-2). Gọi H là chân đường cao

Ôn tập chương 3

Bài 3.55 trang 167 Sách bài tập Hình học 10: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0;2), B(-2;-2) và C(4;-2). Gọi H là chân đường cao kẻ từ B; M và N lần lượt là trung điểm của các cạnh AB và BC. Viết phương trình đường tròn đi qua các điểm H, M, N.

Lời giải:

    (Xem hình 3.18)

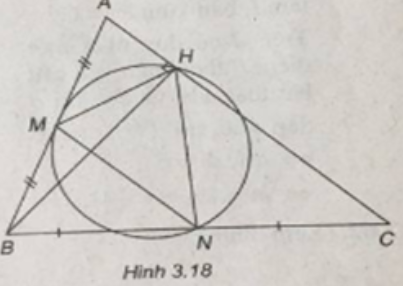
    Ta có: M(-1; 0), N(1; -2), AC = (4; -4)

    Giả sử H(x;y). Ta có :

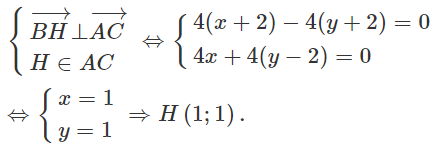
    Giả sử phương trình đường tròn cần tìm là:

    x² + y² + 2ax + 2by + c = 0

    Thay tọa độ của M, N, H vào (1) ta có hệ điều kiện :

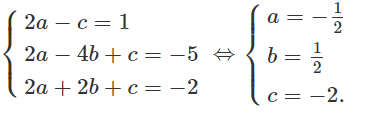
    Vậy phương trình đường tròn cần tìm là: x² + y² - x + y - 2 = 0