Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x^2 + y^2 - 2x - 2y + 1 = 0 và đường thẳng d: x - y + 3 = 0

Ôn tập chương 3

Bài 3.60 trang 167 Sách bài tập Hình học 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x² + y₂ - 2x - 2y + 1 = 0 và đường thẳng d: x - y + 3 = 0. Tìm tọa độ điểm M nằm trên d sao cho đường tròn tâm M có bán kính gấp đôi bán kính đường tròn (C) và tiếp xúc ngoài với đường tròn (C).

Lời giải:

    (Xem hình 3.22)

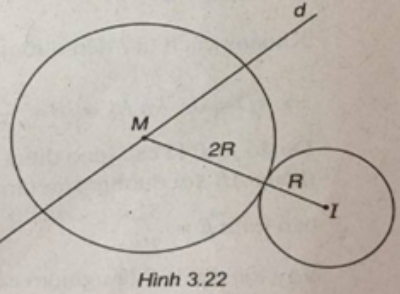
    Đường tròn (C) có tâm I(1; 1), bán kính R = 1.

    Vì M ∈ d nên M(x; x + 3). Yêu cầu của bài toán tương đương với:

    MI = R + 2R ⇔ (x - 1)² + (x + 2)² = 9

    ⇔ x = 1; x = 2

    Vậy có hai điểm M thỏa mãn yêu cầu bài toán là M(1; 4) và M(-2; 1).