Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng: d1: x - y = 0 và d2 = 2x + y - 1 = 0

Ôn tập chương 3

Bài 3.58 trang 167 Sách bài tập Hình học 10: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng: d₁: x - y = 0 và d₂ = 2x + y - 1 = 0. Tìm tọa độ các đỉnh hình vuông ABCD biết rằng đỉnh A thuộc d₁, đỉnh C thuộc d₂ và các đỉnh B, D thuộc trục hoành.

Lời giải:

    (Xem hình 3.21)

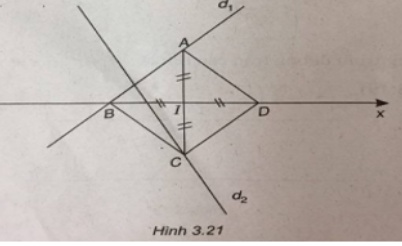
    Vì A ∈ d₁ ⇒ A(t; t)

    Vì A và C đối xứng nhau qua BD và B, D ∈ Ox nên C(t; -t)

    Vì C ∈ d₂ nên 2t - t - 1 = 0 ⇔ t = 1. Vậy A(1; 1), C(1; -1).

    Trung điểm AC là I(1; 0). Vì I là tâm hình vuông nên

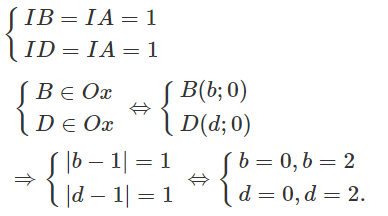
    Suy ra B(0; 0) và D(2; 0) hoặc B(2; 0), D(0; 0).

    Vậy bốn đỉnh của hình vuông là A(1; 1), B(0; 0), C(1; -1), D(2; 0)

    hoặc A(1; 1), B(2; 0), C(1; -1), D(0; 0).