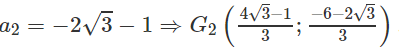Trong mặt phẳng tọa độ Oxy,xét tam giác ABC vuông tại A, phương trình đường thẳng BC

Ôn tập chương 3

Bài 3.63 trang 168 Sách bài tập Hình học 10: Trong mặt phẳng tọa độ Oxy,xét tam giác ABC vuông tại A, phương trình đường thẳng BC là: √3x - y - √3 = 0, các đỉnh A và B thuộc trục hoành và bán kính đường tròn nội tiếp tam giác bằng 2. Tìm tọa độ trọng tâm G của tam giác ABC.

Lời giải:

    Ta có: BC ∩ Ox ≡ B(1; 0)

    Đặt x_A = a ta có A(a;0) và x_C = a ⇒ y_C = √3a - √3

    Vậy C(a; √3a - √3)

    Từ công thức

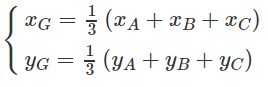
    Ta có:

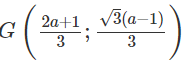
    Mà AB = |a - 1|, AC = √3|a - 1|, BC = 2|a - 1|. Do đó:

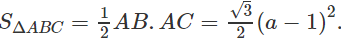
    Ta có:

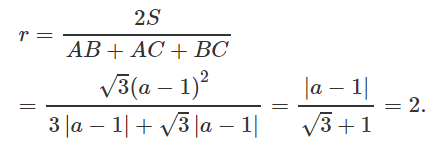
    Trường hợp 1.

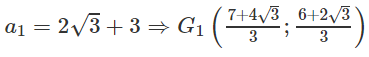
    Trường hợp 2.