Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 1)^2 + (y - 2)^2 = 4 và đường thẳng d

Ôn tập chương 3

Bài 3.61 trang 168 Sách bài tập Hình học 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 1)² + (y - 2)² = 4 và đường thẳng d: x - y - 1 = 0. Viết phương trình đường tròn (C ') đối xứng vơi đường tròng (C) qua đường thẳng d. Tìm tọa độ các giao điểm của (C) và (C').

Lời giải:

    (Xem hình 3.23)

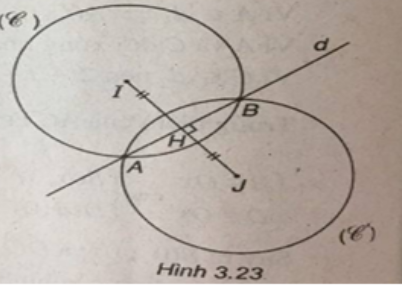
    Đường thẳng d có vectơ pháp tuyến là n(1; -1). Do đó đường thẳng Δ đi qua tâm I(1; 2) và vuông góc với d có phương trình :

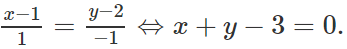
    Tọa độ giao điểm H của d và là nghiệm của hệ phương trình :

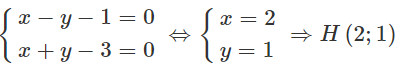
    Gọi J là điểm đối xứng của I qua d. Khi đó :

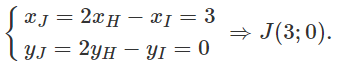
    Vì (C') đối xứng với (C ) qua d nên (C') có tâm là J(3; 0) và bán kính R = 2.

    Do đó (C') có phương trình là: (x - 3)² + y² = 4

    Tọa độ các giao điểm của (C ) và (C') là nghiệm của hệ phương trình :

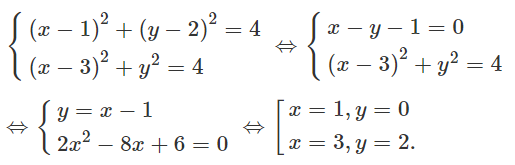
    Vậy tọa độ giao điểm của (C ) và (C') là A(1; 0) và B(3; 2).