Cho ba điểm A(1; 4), B(3; 2), C(5; 4). Tọa độ tâm đường tròn ngoại tiếp tam giác ABC là
Ôn tập chương 3
Bài tập trắc nghiệm trang 168, 169, 170, 171, 172 Sách bài tập Hình học 10:
Bài 3.65: Cho ba điểm A(1; 4), B(3; 2), C(5; 4). Tọa độ tâm đường tròn ngoại tiếp tam giác ABC là:
A. (2;5) B. (3/2;2)
C. (9;10) D. (3;4)
Lời giải:
BA→ = (-2; 2), BC→ = (2; 2)
BA→. BC→ = 0 ⇒ ∠(ABC) = 90o.
Đường tròn ngoại tiếp có tâm là trung điểm I của AC nên có tọa độ (3;4).
Đáp án: D
Bài 3.66: Cho đường thẳng Δ có phương trình tham số
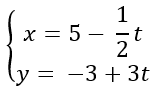
Một vectơ chỉ phương của Δ có tọa độ là:
A. (-1;6) B. (1/2;3)
C. (5;-3) D. (-5;3)
Lời giải:
Đáp án: A
Bài 3.67: Cho đường thẳng d: 3x - 2y + 12 = 0, Δ là đường thẳng song song với đường thẳng d và cắt Ox, Oy lần lượt tại A, B sao cho AB = √13. Phương trình của Δ là:
A. 3x - 2y + 12 = 0
B. 3x - 12 - 12 = 0
C. 6x - 4y - 12 = 0
D. 3x - 4y - 6 = 0
Lời giải:
Đường thẳng Δ: 6x – 4y – 12 = 0 cắt Ox và Oy lần lượt tại A(2;0) và B(0; -3).
Ta có AB = √13.
Đáp án: C
Bài 3.68: Cho đường thẳng Δ có phương trình tham số
. Điểm nào sau đây nằm trên đường thẳng Δ?
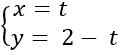
A. (1;1) B. (0;-2)
C. (1;-1) D. (-1;1)
Lời giải:
Đáp án: A
Bài 3.69: Đường thẳng đi qua điểm M(1;2) và song song với đường thẳng d: 4x + 2y + 1 = 0 có phương trình tổng quát là:
A. 4x + 2y + 1 = 0 B. 2x + y + 4 = 0
C. 2x + y - 4 = 0 D. x - 2y + 3 = 0
Lời giải:
Đường thẳng Δ: 2x + y – 4 = 0 song song với đường thẳng d: 4x + 2y + 1 = 0 và đi qua điểm M(1;2).
Đáp án: C
Bài 3.70: Cho đường thẳng d có phương trình tổng quát: 3x + 5y + 2017 = 0. Khẳng định nào sau đây là sai?
A. d có vectơ pháp tuyến n = (3;5).
B. d có vectơ chỉ phương u = (5;-3).
C. d có hệ số góc k = 5/3.
D. d song song với đường thẳng 3x + 5y = 0
Lời giải:
Đường thẳng Δ: 3x + 5y + 2017 = 0 có hệ số góc là k = (-3)/5. Phát biểu C sai.
Đáp án: C
Bài 3.71: Hình chiếu vuông góc của điểm M(1;4) xuống đường thẳng Δ: x - 2y + 2 = 0 có tọa độ là:
A. (3;0) B. (0;3)
C. (2;2) D. (2;-2)
Lời giải:
Điểm C(2;2) có tọa độ thỏa mãn phương trình đường thẳng Δ: x – 2y + 2 = 0.
Ta lại có MC→ = (1; -2), nΔ→ = (1; -2) suy ra MC vuông góc với Δ. Vậy C(2;2) là hình chiếu vuông góc của M xuống Δ.
Đáp án: C
Bài 3.72: Đường thẳng đi qua hai điểm A(1;1), B(2;2) có phương trình tham số là:
Lời giải:
Đường thẳng Δ đi qua A(1;1), B(2;2) có vectơ chỉ phương AB→ = (1;1).
Vậy Δ có phương trình tham số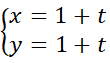 
Điểm O(0;0) thỏa mãn phương trình của Δ (ứng với t = -1). Vậy phương trình tham số của Δ có thể viết là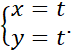 
Đáp án: D
Bài 3.73: Đường tròn (C) có tâm là gốc O(0;0) và tiếp xúc với đường thẳng Δ: 8x + 6y + 100 = 0. Bán kính của đường tròn (C) là:
A. 4 B. 6 C. 8 D. 10
Lời giải:
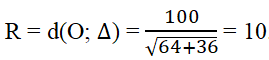
Đáp án: D
Bài 3.74: Góc giữa hai đường thẳng: Δ1: x + 2y + 4 = 0 và Δ2: x - 3y + 6 = 0
A. 30ο B. 60ο C. 45ο D. 23ο12'
Lời giải:
cos(Δ1, Δ2) = 1/√2.
Đáp án: C
Bài 3.75: Cho hai đường thẳng Δ1 và Δ2 lần lượt có phương trình x - y = 0 và √3x - y = 0. Góc giữa Δ1 và Δ2 có số đo là:
A. 30ο B. 15ο C. 45ο D. 75ο
Lời giải:
(Ox, Δ1) = 45o, (Ox, Δ2) = 60o. Suy ra (Δ1, Δ2) = 15o.
Đáp án: B
Bài 3.76: Phương trình nào trong các phương trình sau đây không là phương trình đường tròn?
A. x2 + y2 - 4 = 0
B. x2 + y2 - 4x + 4 = 0
C. x2 + y2 + 4x - 4y + 4 = 0
D. x2 + y2 - 2x - 2y + 1 = 0
Lời giải:
Phương trình x2 + y2 + x + y + 2 = 0 không là phương trình của đường tròn vì không thỏa mãn điều kiện a2 + b2 – c > 0.
Đáp án: B
Bài 3.77: Cho ba điểm A(-2;0), B(√2;√2), C(2;0). Đường tròn ngoại tiếp tam giác ABC có phương trình là:
A. x2 + y2 - 4 = 0
B. x2 + y2 - 4x + 4 = 0
C. x2 + y2 + 4x - 4y + 4 = 0
D. x2 + y2 = 2
Lời giải:
Tọa độ ba điểm A(-2;0), B(√2; √2), C(2;0) đều thỏa mãn phương trình đường tròn x2 + y2 = 4.
Đáp án: A
Bài 3.78: Cho hai điểm A(3;0), B(0;4). Đường tròn nội tiếp tam giác OAB có phương trình là:
A. x2 + y2 = 1
B. x2 + y2 = 2
C. x2 + y2 - 2x - 2y + 1 = 0
D. x2 + y2 - 6x - 8y + 25 = 0
Lời giải:
Đường tròn nội tiếp tam giác OAB có tâm I(a;a). Ta có d(I, AB) = d(I, Ox) suy ra I(1;1). Ta có R = d(I, Ox) = 1. Vậy phương trình của đường tròn nội tiếp tam giác OAB là: x2 + y2 – 2x – 2y + 1 = 0.
Đáp án: C
Bài 3.79: Cho hai đường tròn:
(C1): x2 + y2 + 2x - 6y + 6 = 0
(C2): x2 + y2 - 4x + 2y - 4 = 0
Tìm khẳng định đúng trong các khẳng định sau:
A. (C1) cắt (C2).
B. (C1) không có điểm chung với (C2).
C. (C1) tiếp xúc trong với (C2).
D. (C1) tiếp xúc ngoài với (C2).
Lời giải:
(C1) có tâm I1(-1;3) và bán kính R1 = 2.
(C2) có tâm I2(2; -1) và bán kính R2 = 3.
Ta có I1I2 = R1 + R2. Vậy (C1) tiếp xúc ngoài với (C2).
Đáp án: D
Bài 3.80: Tiếp tuyến với đường tròn (C): x2 + y2 = 2 tại điểm M0(1;1) có phương trình là:
A. x + y - 2 = 0 B. x + y + 1 = 0
C. 2x + y - 3 = 0 D. x - y = 0
Lời giải:
Tiếp tuyến Δ có vectơ pháp tuyến OMo→ = (1;1).
Phương trình Δ có dạng 1.(x – 1) + 1.(y – 1) = 0 hay x + y – 2 = 0.
Đáp án: A
Bài 3.81: Số đường thẳng đi qua điểm M(5;6) và tiếp xúc với đường tròn (C): (x - 1)2 + (y - 2)2 = 1 là:
A. 0 B. 1 C. 2 D. 3
Lời giải:
IM > R suy ra điểm M nằm ngoài đường tròn
Đáp án: C
Bài 3.82: Có bao nhiêu tiếp tuyến với đường tròn (C): x2 + y2 - 8x - 4y = 0 đi qua gốc tọa độ?
A. 0 B. 1 C. 2 D. 3
Lời giải:
Đường tròn (C) đi qua gốc O(0;0).
Đáp án: B
Bài 3.83: Cho elip (E) có hai tiêu điểm là F1, F2 và có độ dài trục lớn bằng 2a. Trong các khẳng định sau, khẳng định nào đúng?
A. 2a = F1F2 B. 2a > F1F2
C. 2a < F1F2 D. 4a = F1F2
Lời giải:
Đáp án: B
Bài 3.84: Một elip (E) có phương trình chính tắc
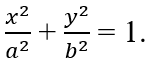
Gọi 2c là tiêu cự của (E). Trong các khẳng định sau, khẳng định nào đúng?
A. c2 = a2 + b2 B. b2 = a2 + c2
C. a2 = b2 + c2 D. c = a + c
Lời giải:
Đáp án: C
Bài 3.85: Cho điểm M(2;3) nằm trên đường elip (E) có phương trình chính tắc:
. Trong các điểm sau đây điểm nào không nằm trên elip (E):
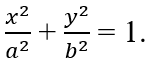
A. M1(-2;3) B. M2(2;-3)
C. M3(-2;-3) D. M4(3;2)
Lời giải:
(E) đi qua các điểm M1, M2, M3.
Đáp án: D
Bài 3.86: Cho elip (E) có phương trình chính tắc
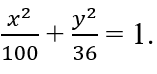
Trong các điểm có tọa độ sau đây điểm nào là tiêu điểm của elip (E)?
A. (10;0) B. (6;0) C. (4;0) D. (-8;0)
Lời giải:
Đáp án: D
Bài 3.87: Cho elip (E) có tiêu điểm F1(4;0) và có một đỉnh A(5;0). Phương trình chính tắc của (E) là:
Lời giải:
Đáp án: C
Bài 3.88: Elip (E):
và đường tròn (C): x2 + y2 = 25 có bao nhiêu điểm chung?
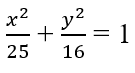
A. 0 B. 1 C. 2 D. 3
Lời giải:
(C) tiếp xúc với (E) tại A1(-5;0) và A2(5;0).
Đáp án: C
Bài 3.89: Cho elip (E):
và đường thẳng Δ: y = 3. Tích các khoảng cách từ hai tiêu điểm của (E) đến Δ bằng giá trị nào sau đây?
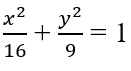
A. 16 B. 9 C. 81 D. 7
Lời giải:
d(F1, Δ) x d(F2, Δ) = b2 = 9.
Đáp án: B
Bài 3.90: Đường tròn đi qua ba điểm A(0;3), B(-3;0), C(3;0) có phương trình là:
A. x2 + y2 = 0
B. x2 + y2 - 6x - 6y + 9 = 0
C. x2 + y2 - 6x + 6y = 0
D. x2 + y2 - 9 = 0
Lời giải:
OA = OB = OC = 3.
Đường tròn ngoại tiếp tam giác ABC có phương trình x2 + y2 – 9 = 0.
Đáp án: D
Bài 3.91: Với giá trị nào của m thì đường thẳng Δ:
tiếp xúc với đường tròn x2 + y2 = 1?
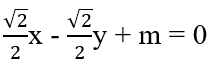
A. m = 1 B. m = 0
C. m = √2 D. m = √2/2
Lời giải:
Δ tiếp xúc với đường tròn tâm O bán kính R = 1 ⇔ d(O; Δ) = 1 ⇔ |m| = 1.
Đáp án: A
Bài 3.92: Tiếp điểm của đường thẳng d: x + 2y - 5 = 0 với đường tròn (C): (x - 4)2 + (y - 3)2 = 5 là:
A. (3;1) B. (6;4)
C. (5;0) D. (1;2)
Lời giải:
Viết phương trình đường thẳng d’ đi qua tâm I(4;3) của đường tròn (C) và vuông góc với đường thẳng d ta được d’: 2x – y – 5 = 0. Hai đường thẳng d và d’ cắt nhau tại tiếp điểm M(3;1).
Đáp án: A
Bài 3.93: Với giá trị nào của m thì phương trình sau đây là phương trình của đường tròn x2 + y2 - 2(m + 2)x + 4my + 19m - 6 = 0?
A. 1 < m < 2 B. -2 ≤ m ≤ 1
C. m < 1 hay m > 2 D. m < -2 hay m > 1
Lời giải:
Giải điều kiện a2 + b2 – c > 0 ta được: m < 1 hay m > 2.
Đáp án: C
