Bài 1, 2, 3, 4, 5, 6, 7 trang 137 SBT Toán 7 tập 1

Bài 1, 2, 3, 4, 5, 6, 7 trang 137 SBT Toán 7 tập 1

Bài 1: Tính giá trị x ở hình dưới:

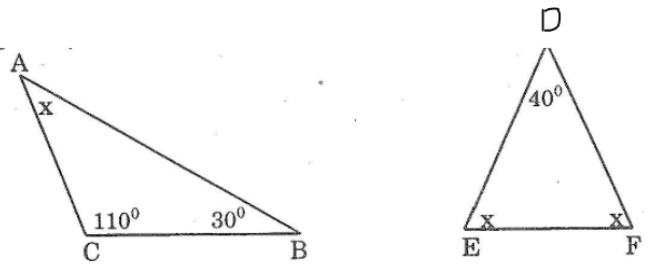
Lời giải:

Trong ΔABC ta có:

∠A +∠B + ∠C = 180°(tổng ba góc trong tam giác)

∠A = 180° - (∠B + ∠C )

x = 180° - (30° + 110°) = 40°

Trong ΔDEF có:

∠D +∠E +∠F = 180° (tổng ba góc trong tam giác)

Mà ∠E = ∠F (gt)

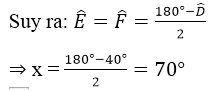
Bài 2: Cho tam giác ABC có ∠A = 60°,∠C = 50°. Tia phân giác của góc B cắt AC ở D. Tính ∠ADB ,∠CDB

Lời giải:

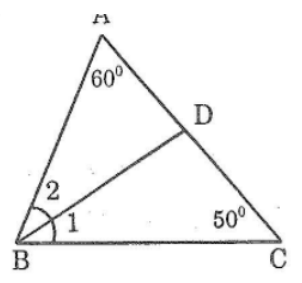
Trong ΔABC ta có:

∠A +∠B +∠C =180o(tổng ba góc trong tam giác)

⇒ ∠B = 180° - (∠A + ∠C )

⇒ x = 180° - (60° + 50°) = 70°

(∠B1) =(∠B2 ) =(1/2 )∠B (vì BD là tia phân giác)

⇒ ∠B = 70° : 2 = 35°

Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D

⇒ ∠(ADB) =∠(B1 ) +∠C (tính chất góc ngoài tam giác)

∠(ADB) + ∠(BDC) = 180°(hai góc kề bù)

⇒ ∠(BDC) = 180° - ∠(ADB) = 180° - 85° = 95°

Bài 3: Cho tam giác ABC, điểm M nằm trong ta, giác đó. Tia BM cắt AC ở K.

So sánh ∠(AMK) và ∠(ABK)

So sánh ∠(AMC) và ∠(ABC)

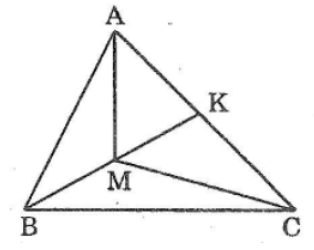
Lời giải:

Trong ΔAMB ta có AMK là góc ngoài tại đỉnh M.

⇒ ∠(AMK) > ∠(ABK) (tính chất góc ngoài tam giác)     (1)

Trong ΔCBM ta có KMC là góc ngoài tại đỉnh M

⇒ ∠(KMC) > ∠(MBC) (tính chất góc ngoài tam giác)     (2)

Cộng từng vế (1) và (2) ta có: ∠(AMK) +∠(KMC) > ∠(ABM) +∠(MBC)

Suy ra: ∠(AMC) > ∠(ABC)

Bài 4: Hãy chọn giá trị đúng của x trong các kết quả A, B, C, D (xem hình dưới , trong đó IK//EF)

A) 100°

B) 70°

C) 80°

D) 90°

Lời giải:

Ta có: IK //EF suy ra ∠IKF + ∠F = 180° (hai góc trong cùng phía)

⇒ ∠ F = 180° - ∠(IKF) =180° - 140° = 40°

Trong ΔOEF ta có góc ngoài tại đỉnh E bằng 130°

⇒ ∠O = 130° - ∠F = 130° - 40° = 90°

Vậy chọn đáp án D

Bài 5: Cho tam giác nhọn ABC. Kẻ BH vuông góc với AC ( H thuộc AC), kẻ CK vuông góc với AB ( K thuộc AC). Hãy so sánh ∠(ABH) và ∠(ACK.)

Lời giải:

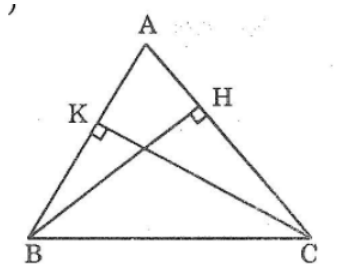
Tam giác nhọn ABH bvuông tại H

⇒ ∠(ABH) + ∠A = 90° (tính chất tam giác vuông)

⇒ ∠(ABH) = 90° - ∠A (1)

Tam giác AC vuông tại K

⇒ ∠(ACK) + ∠A = 90° (tính chất tam giác vuông)

⇒ ∠(ACK) = 90° - ∠A (2)

từ (1) và (2) suy ra: ∠(ACK) = ∠(ABH)

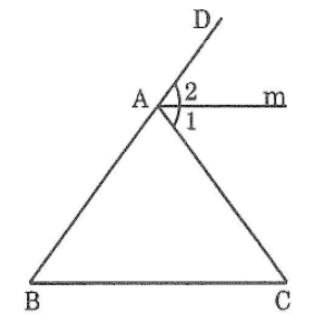
Bài 6: Cho tam giác ABC có ∠B = ∠C = 50°. Gọi Am là tia phân giác của góc ngoaì ở đỉnh A. Hãy chứng tỏ rằng Am // BC.

Lời giải:

Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A

⇒ ∠(CAD ) = ∠B + ∠C = 50 + 50 = 100°

(tính chất góc ngoài tam giác)

∠(A₁ ) = ∠(A₂ ) = 1/2 ∠(CAD) = 50° (vì tia Am là tia phân giác của ∠(CAD)

Suy ra: ∠(A₁) = ∠C = 50°

⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

Bài 7: a, Một góc nhọn của eke bằng 30°. Tính góc nhọn còn lại.

b, Một góc nhọn của eke bằng 45°.tính góc nhọn còn lại

Lời giải:

Vì eke là một tam giác vuông , nên:

Một góc nhọn của eke bằng 30° thì góc còn lại bằng:

90° - 30° = 60°

Một góc nhọn của eke bằng 45° thì góc còn lại bằng:

90° - 45° = 45°