Bài 16, 17, 18 trang 139 SBT Toán 7 tập 1

Bài 16, 17, 18 trang 139 SBT Toán 7 tập 1

Bài 16: Cho tam giác ABC có A = 90°, kẻ AH vuông goác với BC (H thuộc BC). Các tia phân giác của ∠C và ∠BAH cắt nhau ở I. chứng minh rằng: ∠(AIC) = 90°

Lời giải:

Ta có: AH ⊥ BC (gt) ⇒ ΔAHB vuông tại H

Trong tam giác vuông AHB ta có: ∠BHA = 90°

⇒ B + ∠BAH = 90°     (1)

Trong tam giác vuông ABC ta có: ∠BAC = 90°

⇒ B + ∠C = 90°     (2)

Từ (1) và (2) suy ra: ∠BAH = ∠C

∠A₁ = ∠A₂ = 1/2.∠BAH (gt)

∠C₁ = ∠C₂ = 1/2.∠C (gt)

Suy ra

∠A₁ = ∠A₂ = ∠C₁ = ∠C₂

∠A₁ + ∠IAC = 90°

Suy ra:

∠C₁ + ∠IAC = 90°

Trong ΔAIC có:

∠C₁ + ∠IAC = 90°

Vậy:

∠IAC = 9°

Bài 17: Chứng minh rằng nếu một đường thẳng song song thì hai tia phân giác của các cặp góc trong cùng phía vuông goác với nhau.

Lời giải:

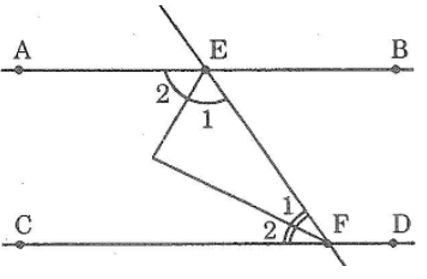
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F

Ta có: ∠BEF + ∠EFD = 180° (hai góc trong cùng phía)

E₁ = 1/2 (BEF) =(gt)

F₁ = 1/2 ∠EFD = (gt)

⇒ E₁ +F₁ = 1/2 (∠BEF + ∠EFD ) = 90°

Trong ΔEKF,ta có:

∠EKF = 180° - (E₁ +F₁) = 180° - 90° = 90°

Vậy EK ⊥ FK

Bài 18: Cho tam giác ABC có: B - C = 20°. Tia phân giác của góc A cắt BC tại D. tính số đo các góc (ADC) , (ADB)

Lời giải:

Trong ΔABD ta có ∠D₁ là góc ngoài tại đỉnh D

∠D₁ = B + ∠A₁ (tính chất góc ngoài củ tam giác)

Trong ΔADC ta có ∠D₂ là góc ngoài tại đỉnh D

∠D₂ = C + ∠A₂ (tính chất góc ngoài của tam giác)

Ta có: ∠B > ∠C (gt); ∠A₁ = ∠A₂ (gt)

⇒ ∠D₁ -∠D₂ = (B + ∠A₁) - (C + ∠A₂) = ∠B - ∠C = 20°

∠D₁ + ∠D₂ = 180° (hai góc kề bù)

⇒ ∠D₁ = (180° + 20°) : 2 = 100°

⇒ ∠D₁ = (100° - 20°) = 80°