Bài 8, 9, 10, 11, 12, 13, 14, 15 trang 138 SBT Toán 7 tập 1

Bài 8, 9, 10, 11, 12, 13, 14, 15 trang 138 SBT Toán 7 tập 1

Bài 8: Cho tam giác ABC có ∠A = 100°, ∠B - ∠C = 20°. Tính ∠B và∠ C

Lời giải:

Trong ΔABC, ta có:

∠A + ∠B + ∠C = 180° (tổng ba góc trong tam giác)     (1)

∠B - ∠C = 20°     (2)

Từ (1) và (2) suy ra: 2B = 100° ⇒ B = 50°

Vậy: ∠C = 80° - 50° = 30°

Bài 9: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Tìm góc B.

Lời giải:

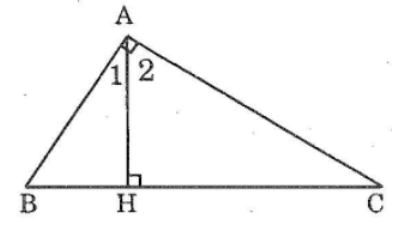
Có thể tìm góc B bằng hia cách:

Cách 1

Ta có: ∠(A₁ ) +∠(A₂ ) = ∠(BAC) = 90° (1)

Vì ΔAHB vuông tại H nên :

∠B +∠(A₁ ) = 90°(tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra ∠B = ∠(A₂ )

Cách 2

Vì ΔABC vuông tại A nên:

∠B +∠C = 90° (theo tính chất tam giác vuông) (1)

Vì ΔAHC vuông tại H nên:

∠(A₂ ) + ∠C = 90° (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B = ∠(A₂ )

Bài 10: Cho hình dưới:

a. Có bao nhiêu tam giác vuông trong hình?

b. Tính số đo các góc nhọn ở các đỉnh C,D,E

Lời giải:

Có 5 tam giác vuông trong hình:

ΔABC vuông tại B

Δ CDB vuông tại B

Δ EDA vuông tại D

Δ DCA vuông tại C

Δ DCE vuông tại C

ΔABC vuông tại B suy ra:

∠A + ∠(ACB) = 90° (theo tính chất tam giác vuông)

⇒ ∠(ACB) = 90° - ∠A = 90° - 40° = 50°

∠(ACB) + ∠(BCD) = ∠(ACD) = 90°

⇒ ∠(BCD) = 90° - ∠(ACB) = 90° - 50° = 40°

ΔACD vuông tại C suy ra:

∠A + ∠(CDA) = 90° (theo tính chất tam giác vuông)

⇒ ∠(CDA) = 90° - ∠A = 90° - 40° = 50°

∠(CDA) + ∠(CDE) =∠(ADE) = 90°

⇒ ∠(CDE) = 90° - ∠(CDA) = 90° - 50° = 40°

ΔDAE vuông tại D suy ra:

∠A + ∠E = 90° (theo tính chất tam giác vuông)

⇒ ∠ E = 90° - ∠A = 90° - 40° = 50°

Bài 11: Cho tam giác ABC có ∠B = 70°; ∠C = 30°. Tia phân giác của góc A cắt BC tại D. kẻ AH vuông góc vói BC (H thuộc BC)

Tính ∠(BAC)

Tính ∠(ADH)

Tính ∠(HAD)

Lời giải:

Trong ΔABC có:

∠(BAC) + ∠B +∠C = 180° (tổng ba góc trong tam giác)

Mà ∠(BAC) + 70° + 30° = 180°

Vậy ∠(BAC) = 180° - 70° - 30° = 80°

Ta có: ∠(A₁ ) = (1/2 )∠(BAC) = (1/2).80° = 40°

(vì Ad tia phân giác của góc BAC)

Trong ΔADC ta có ∠(ADH) là góc ngoài tạ đỉnh D

Do đó: ∠(ADH) = ∠(A₁) +∠C (tính chất góc ngoài của tam giác)

Vậy ∠(ADH ) = 40° + 30° = 70°

ΔADH vuông tại H nên:

∠(HAD) + ∠(ADH) = 90° (tính chất tam giác vuông)

⇒ ∠ (HAD) = 90° - ∠(ADH)° = 90° - 70° = 20°

Bài 12: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. tính ∠(BIC) biết rằng:

∠B = 80°, ∠C = 40°

∠A = 80°

∠A = m°

Lời giải:

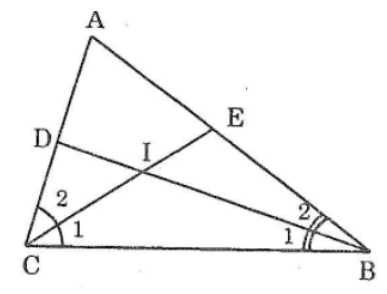
Ta có:

∠(B₁) = (1/2)∠(ABC) = (1/2).80° = 40° (vì BD là tia phân giác ∠(ABC) )

∠(C₁ ) =(1/2)∠(ACB) = (1/2).20° = 10° (vì CE là tia phân giác∠ (ACB) )

Trong ΔIBC, ta có: ∠(BIC) + ∠(B₁ ) + ∠(C₁ ) = 180° (tổng 3 góc trong tam giác)

Vậy: ∠(BIC) = 180° - (∠(B₁ ) + ∠(C₁ ) ) = 180° - (40° + 20°) = 120°

Ta có:

∠(B₁ ) = (1/2)∠ B (vì BD là tia phân giác B )

∠(C₁) = (1/2)C (vì CE là tia phân giác∠( C) )

Trong ΔABC có:

∠(BIC) +∠(B₁ ) + ∠(C₁ ) = 180° (tổng ba goác trong tam giác)

Vậy ∠(BIC) = 180° -((B₁) + ∠(C₁ ) ) = 180° - (∠B + ∠C )/2 = 180° - (100°)/2 = 130°

Ta có:∠B +∠C = 180° - m°

Suy ra: ∠(BIC) = 180° - (180° - m°)/2 = 180 - 90° + (m°)/2 = 90°+ (1/2)m°

Bài 13: Trên hình bên có Ax song sog với By, ∠(CAx) = 50°,∠(CBy) = 40°. Tính ∠(ACB) bằng cách xem nó là góc ngoài của một tam giác.

Lời giải:

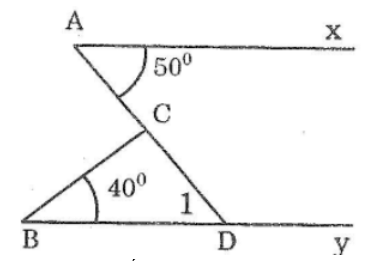
Kéo dài AC cắt By tại D

Vì By // Ax suy ra ∠(D₁ ) =∠A (hai góc so le trong)

Mà ∠A = 50° (gt) nên ∠∠(D₁) = 50°

Trong ΔBCD ta có ∠(ACB) là góc ngoài tại đỉnh C

⇒ ∠(ADC) = ∠B + ∠(D₁ ) (tính chất góc ngoài của tam giác)

⇒ ∠(ADC) = 40° + 50° = 90°

Bài 14: Chứng minh rằng tổng ba goc ngoài ở ba đỉnh của một tam giác thì bằng 360

Lời giải:

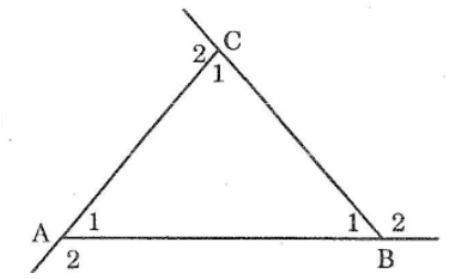
Ta có: ∠(A₁ ) + ∠(A₂ ) = 180°(hai goác kề bù)

∠(B₁ ) + ∠(B₂ ) = 180°(hai góc kề bù)

∠(C₁ ) + ∠(C₂ ) = 180°(hai góc kề bù)

Suy ra: ∠(A₁ ) + ∠(A₂ ) + ∠(B₁) + ∠(B₂ ) + ∠(C₁ ) + ∠(C₂ ) = 180.3 = 540°

⇒ ∠(A₂ ) + ∠( B₂ ) + ∠(C₂ ) = 540° - (∠(A₁ ) + ∠(B₁ ) + ∠(C₁ ) )    (1)

Trong ΔABC, ta có:

∠(A₁ ) + ∠(B₁ ) + ∠(C₁ ) = 180° (tổng ba góc trong tam giác)    (2)

Từ (1) và (2) suy ra: ∠(A₂ ) + ∠(B₂ ) + ∠(C₂ ) = 540° - 180° = 360°

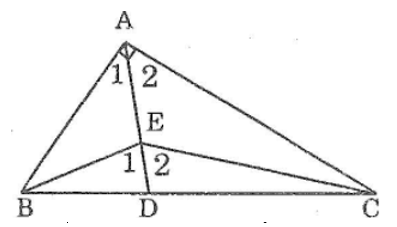
Bài 15: Cho tam giác ABC có ∠A = 90°. Gọi E là trung điểm nằm trên ta giác đó. Chứng minh rằng góc BEC là góc tù.

Kéo dài AE cắt BC tại D

Lời giải:

Trong ΔABE ta có ∠E₁ là góc ngoài tại đỉnh E

Suy ra: ∠E₁ > ∠A₁ (tính chất góc ngoài tam giác)    (1)

Trong ΔAEC ta có ∠E₂ là góc ngoài tại đỉnh E

Suy ra: ∠E₂ > ∠A₂ (tính chất góc ngoài tam giác)    (2)

Cộng từng vế (1) và (2) ta có:

∠E₂ + ∠E₂ > ∠A₂ + ∠A₁

Hay (BEC) > (BAC) = 90°

Vậy (BEC) là góc tù.