Bài 8.1, 8.2, 8.3, 8.4 trang 50 SBT Toán 7 tập 2
Bài 8.1, 8.2, 8.3, 8.4 trang 50 SBT Toán 7 tập 2
Bài 8.1: Cho tam giác cân (không đều) ABC có AB = AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó khẳng định nào sau đây là đúng?
(A) OA > OB;
(B) ∠(AOB) > ∠(AOC) ;
(C) AO ⊥ BC;
(D) O cách đều ba cạnh của tam giác ABC.
Lời giải:
Vì O thuộc đường trung trực của cạnh AB nên OA = OB. Vì ba đường trung trực của một tam giác đồng quy nên OA là đường trung trực của BC, do đó AO ⊥ BC. Vì tam giác ABC cân tại A nên đường trung trực AO đồng thời là đường phân giác của góc A, do đó ΔAOB = ΔAOC, suy ra ∠(AOB) = ∠(AOC) . Do đó tam giác ABC cân tại A nhưng không là tam giác đều nên O không là giao điểm của ba đường phân giác của tam giác ABC. Vậy O không cách đều ba cạnh của tam giác ABC.
Đáp số (C) AO ⊥ BC.
Bài 8.2: Cho tam giác ABC vuông tại A. Gọi P, Q, R lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi O là giao điểm của ba đường phân giác. Khi đó, tâm đường trong ngoại tiếp tam giác ABC là điểm:
(A) O
(B) P;
(C) Q;
(D) R.
Hãy chọn phương án đúng.
Lời giải:
Chọn đáp án D
Bài 8.3: Cho tam giác ABC có ∠A = 100°. Các đường trung trực của AB và AC lần lượt cắt BC ở E và F. Tính ∠(EAF) .
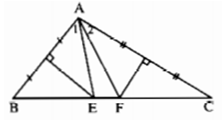
Lời giải:
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra B = (A1 ) . Tương tự, có C = (A2 ) . Ta có:
∠(EAF) = ∠A − (∠A1 + ∠A2 ) = ∠A − (∠B + ∠C )
Mặt khác
∠B + ∠C = 180° − A = 180° − 100° = 80°
Do đó ∠(EAF) = 100° − 80° = 20°.
Bài 8.4: Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB; AC cắt nhau tại O và lần lượt cắt BC tại M, N. Chứng minh rằng AO là tia phân giác của góc MAN.
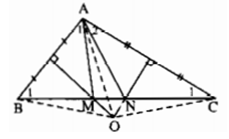
Lời giải:
Theo bài 8.3 ta đã có A1 = B1 , A2 = C2 (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ∠(OAB) = ∠(OBA) , ∠(OAC) = ∠(OCA) , ∠(OBC) = ∠(OCB) . Kết hợp với(1) ∠(OBM) = ∠(OAM) , ∠(OCN) = ∠(OAN) , hay ∠(OAM) = ∠(OBC) = ∠(OCB) = ∠(OAN). Vậy OA là tia phân giác góc MAN.

