Bài 67, 68, 69 trang 50 SBT Toán 7 tập 2

Bài 67, 68, 69 trang 50 SBT Toán 7 tập 2

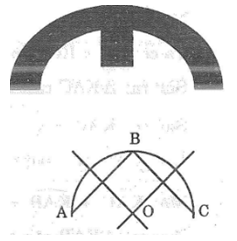
Bài 67: Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy (hình bên). Hãy nêu cách xác định tâm của đường viền.

Lời giải:

Lấy ba điểm A, B, C phân biệt trên đường viền.

Dựng đường trung trực của AB và BC. Hai đường trung trực cắt nhau tại O.

Đoạn OA, OB, OC chính là bán kính của đường viền.

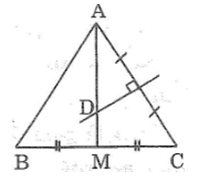
Bài 68: Cho tam giác ABC cân tại A, đường trung tuyến AM. Đường trung trực của AC cắt đường thẳng Am ở D. Chứng minh rằng DA = DB.

Lời giải:

Vì ΔABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.

Vì D là giao điểm của các đường trung trực AC và BC nên D thuộc đường trung trực của AB.

Theo tính chất đường trung trực, ta có:

DA = DB.

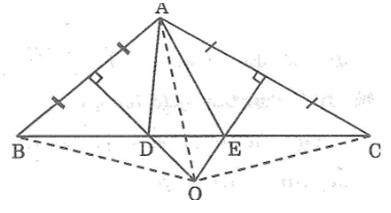
Bài 69: Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E.

a. Các tam giác ABD, ACE là tam giác gì?

b. Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ?

Lời giải:

a. Vì D thuộc đường trung trực của AB nên:

DA = DB (tính chất đường trung trực)

Suy ra: ΔADB cân tại D.

Vì E thuộc đường trung trực của AC nên:

EA = EC (tính chất đường trung trực)

Suy ra: ΔAEC cân tại A.

b. Vì O là giao điểm ba đường trung trực của ΔABC nên:

OA = OB = OC

Vậy (O; OA) đi qua ba điểm A, B, C.