Bài 64, 65, 66 trang 49 SBT Toán 7 tập 2

Bài 64, 65, 66 trang 49 SBT Toán 7 tập 2

Bài 64: Cho tam giác ABC. Tìm một điểm O cách đều ba điểm A, B, C.

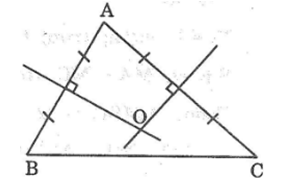
Lời giải:

Vì điểm O cách đều hai điểm A và B nên O thuộc đường trung trực của AB.

Vì điểm O cách đều hai điểm A và C nên O thuộc đường trung trực của AC.

Vì điểm O cách đều hai điểm B và C nên O thuộc đường trung trực của BC.

Trong tam giác, ba đường trung trực đồng quy tại một điểm. Dựng đường trung trực AB và BC cắt nhau tại O.

Vậy O là điểm cần tìm.

Bài 65: Cho hình dưới (hình 65a). Chứng minh rằng ba điểm B, K, C thẳng hàng

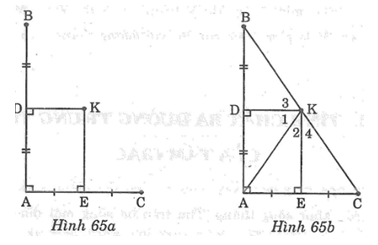
Lời giải:

Nối KA, KB, KC (hình 65b).

Vì KD là đường trung trực của AB nên:

KA = KB (tính chất đường trung trực)

Suy ra: ΔKAB cân tại K

Do đó KD là đường phân giác của ∠(AKB)

Suy ra: ∠K₁ = ∠K₃ ⇒ ∠(AKB) = 2 ∠K₁    (1)

Vì KE là đường trung trực của AC nên:

KA = KC (tính chất đường trung trực)

Do đó KE là đường phân giác của ∠(AKC)

Suy ra: ∠K₂ = ∠K₄ ⇒ ∠(AKC) = 2 ∠K₂    (2)

Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)

Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)

Lại có: KE ⊥ AC (gt)

Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)

Hay: ∠(DKE) = 90° ⇒ ∠K₁ +∠K₂ = 90°

Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K₁ + 2∠K₂

= 2.( ∠K₁ +∠K₂ ) = 2.90° = 180°.

Vậy B, K, C thẳng hàng.

Bài 66: Dựa vào kết quả của bài 65, hãy chứng minh rằng:

a. Các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.

b. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

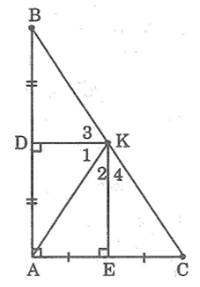
Lời giải:

a. Kẻ đường trung trực của AC cắt BC tại K

Nối AK.

Ta có: KA = KC (tính chất đường trung trực)

Suy ra: Δ KAC cân tại K

Suy ra: ∠(KAC) = ∠C    (1)

Lại có: ∠C + ∠B = 90° (t/chất tam giác vuông)    (2)

Mà: ∠(KAC) + ∠(KAB) = ∠(BAC) = 90°    (3)

Suy ra: Δ KAB cân tại K ⇒ KA = KB

Suy ra: K thuộc đường trung trực của AB

Do đó K là giao điểm ba đường trung trực của Δ ABC

Suy ra: KB = KC = KA ⇒ K là trung điểm của BC

Vậy các đường trung trực của tam giác vuông đi qua trung điểm cạnh huyền

b. Giả sử Δ ABC có ∠A = 90°.

Gọi M là trung điểm của BC.

Trên tia đối của tia MA lấy điểm D sao cho MD = MA

Xét Δ AMC và Δ BMD, ta có:

BM = CM (gt)

∠(AMC) = ∠(BMD) (đối đỉnh)

MA = MD (theo cách vẽ)

Suy ra: Δ AMC = Δ BMD (c.g.c) ⇒ ∠(MAC) = ∠D (hai góc tương ứng)

Suy ra: BD // AC (vì có cặp góc so le trong bằng nhau)

Mà: AC ⊥ AB (gt)

Suy ra: BD ⊥ AB hay ∠(ABD) = 90°

Xét Δ ABC và Δ BAD, ta có:

∠(BAC) = ∠(ABD) = 90°

AB cạnh chung

BD = AC (vì Δ AMC = Δ BMD)

Suy ra: Δ ABC = Δ BAD (c.g.c) ⇒ AD = BC

Mà AM = MD = 1/2 AD nên AM = 1/2 BC

Vậy trong tam giác vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền.